Анализ переходного процесса в линейной электрической
RL-цепи с конечным числом сосредоточенных элементов
Введение
Как известно из основ теории цепей переходный процесс в электрической цепи с конечным числом сосредоточенных линейных двухполюсных элементов при t ³ 0 описывается системой n линейных обыкновенных дифференциальных уравнений для переменных её состояния. Решение этой системы уравнений однозначно, если известны начальные значения n переменных состояния цепи. В качестве переменных состояния цепи выбирают токи её катушек и напряжения её конденсаторов.
В общем случае уравнения для переменных состояния цепи могут быть записаны в матричной форме (в нормальной форме, форме Коши)
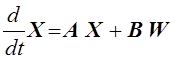 ,
,
где X = X(t) и W = W(t) – векторы переменных состояния цепи (независимых переменных цепи) и воздействий (задающих напряжений и токов),
![]() ,
, ![]() ,
,
n – общее число независимых энергоёмких элементов (катушек и конденсаторов) цепи,
m – общее число источников напряжения и тока цепи,
A и B – матрицы, элементы которых выражаются через параметры R, L и C пассивных элементов цепи,
![]() ,
, ![]() .
.
Если известны X(0+) и W(t) для
любого ![]() , то последующие значения переменных состояния
цепи X(t) определяются
однозначно.
, то последующие значения переменных состояния
цепи X(t) определяются
однозначно.
Вектор Y = Y(t) зависимых переменных (величин, не совпадающих с переменными состояния), находится как линейная комбинация векторов переменных состояния и воздействий:
![]() .
.
Если k – число искомых зависимых величин, то
![]() ,
, ![]() ,
, ![]() .
.
Уравнения для переменных состояния цепи, образующие систему дифференциальных уравнений, можно решить аналитически и численно.
Аналитические методы решения рассматриваются в курсе высшей математики и предполагаются известными.
В среде Mathcad реализовано несколько алгоритмов численного решения задачи Коши для нормальных систем обыкновенных дифференциальных уравнений на отрезке (методы Рунге–Кутта с постоянным (фиксированным) и с переменным (автоматически выбираемым) шагом, метод Булирша–Штера, метод Розенброка). Аргументами функций, реализующих эти алгоритмы, являются: вектор стартовых условий X(0+), начальная и конечная точки отрезка интегрирования, число узлов на этом отрезке и имя вектора-функции, содержащей выражения для производных искомого решения.
Примечания:
1.
Начало отсчёта относительного
времени t совмещают либо с моментом коммутации, либо с моментом
появления определённого значения задающего напряжения ![]() или
тока
или
тока ![]() цепи.
цепи.
2. На схеме цепи ключ изображён в исходном состоянии (перед коммутацией).
3. По умолчанию, до коммутации цепь находится в стационарном состоянии или в установившемся (периодическом, в частности, гармоническом) процессе.
4. Значения аргументов гармонических функций выражаются в радианах.
5. Начальные значения переменных состояния цепи равны нулю, если иное не следует из условия задачи.
Литература
1. Основы теории цепей / Зевеке Г.В., Ионкин П.А., Нетушил А.В. и др. – М., 1989.
2. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. – 4-е изд. – М.: Энергия, 1975.
Литература по Mathcad,у
3. Mathcad 6 Plus. Финансовые, инженерные и научные расчёты в среде Windows 95 / Пер. с англ. – М.: Филин, 1996.
4. Плис А.И., Сливина Н.А. Mathcad: Математический практикум для экономистов и инженеров: Учеб. пособие. – М.: Финансы и статистика, 1999. – 656 с.
5. Плис А.И., Сливина Н.А. Mathcad 2000. – Математический практикум для экономистов и инженеров: Учеб. пособие. – М.: Финансы и статистика, 2000. – 656 с.
6. Херхагер М., Партоль Х. Mathcad 2000: полное руководство / Пер. с нем. – Киев: Ирина, 2000.
7. Дьяконов В.П. Справочник по Mathcad Plus 7 Pro. – М.: СК Пресс, 1998.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.