Экономика и менеджмент \ Организация, планирование и управление строительством

Определение оптимального плана перевозок грузов для строительства (решение транспортной задачи в матричной форме), страница 4

№ варианта

Наличие (Аi) и расход (В¢i, В¢¢i)ресурсов

арматура

пиломатериалы

цемент

плитка

трудозатраты

А1

В¢1

В¢¢1

А2

В¢2

В¢¢2

А3

В¢3

В¢¢3

А4

В¢4

А5

В¢5

В¢¢5

1

900

0,5

1,1

520

0,7

0,2

8000

4

9

400

0,6

62000

60

40

Составляю уравнения для нахождения целевой функции, где х1 и х2- количество квартир в кирпичных и крупнопанельных домах.


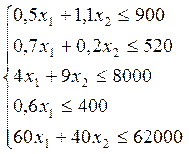
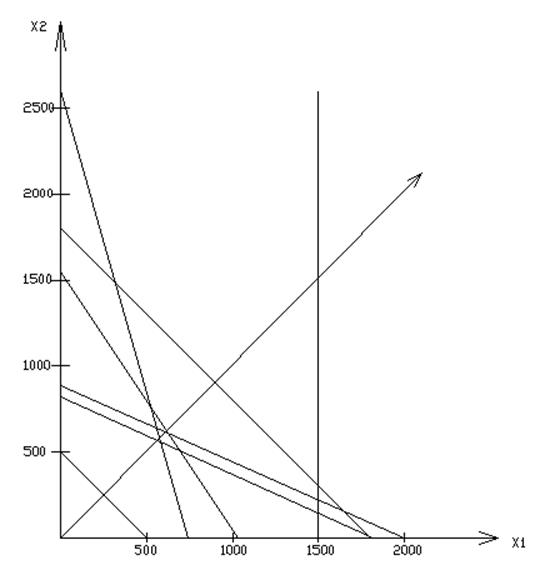
Для решения системы неравенств воспользуюсь графическим методом. Нахожу координаты точек пересечения прямых ограничивающих область решения неравенств, которые будут удовлетворять условию целевой функции.

Преобразую выражения:


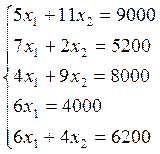
Целевая функция пересекает прямые с уравнениями 1 и 2.

          

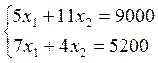
        х1 = 590 и х2 = 550

         Значение целевой функции L = 590 + 550 = 1140.

Использование получаемых ресурсов

Наименование ресурсов

Количество ресурсов

в наличии

использовано

остаток

Арматура

900

900

-

Пиломатериалы

520

520

-

Цемент

8000

7310

+690

Плитка

400

354

+46

Трудозатраты

62000

57400

+4600

ЗАДАЧА №4

Выбор оптимального соотношения длины дорог разного типа

Условия задачи: магистральные дороги области строятся двух типов- с асфальтобетонным и бетонным верхним покрытием.

Требуется определить, сколько километров дорог различного типа надо построить при условии максимального использования наличных ресурсов и получения максимальной прибыли.

№ варианта

Наличие (Аi) и расход (В¢i, В¢¢i)ресурсов

прибыль

асфальт

бетон

песок

гравий

С1

С2

А1

В¢1

В¢¢1

А2

В¢2

В¢¢2

А3

В¢3

В¢¢3

А4

В¢4

В¢¢4

1

15

0,5

-

34

-

1,1

38

1,1

1,2

43

1,2

2,4

3

2

Составляю уравнения для нахождения целевой функции где х1 и х2- длина дороги, асфальтобетонной или бетонной.

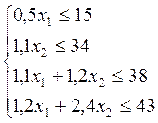
Целевая функция: L = С1 × х1 + С2 × х2 = 3×х1 + 2×х2 à max

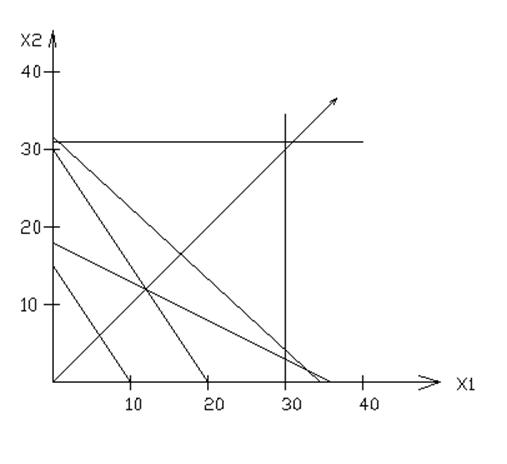
Для решения системы неравенств воспользуюсь графическим методом. Нахожу координаты точек пересечения прямых ограничивающих область решения неравенств, которые будут удовлетворять условию целевой функции.

Преобразую выражения:

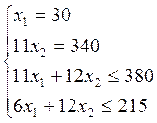
Целевая функция пересекает прямые с уравнениями 1 и 2.

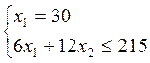                        х1 = 30 и х2 = 5,83

 ед.прибыли

Использование наличных ресурсов

Наименование ресурсов

Количество ресурсов

в наличии

использовано

остаток

Асфальтобетон

15

15

-

Бетон

34

6,41

+27,86

Песок

38

33,2

+4,8

Гравий

43

43

-

 

ЗАДАЧА №5

Определение оптимального плана перевозок грузов для строительства (решение транспортной задачи в сетевой форме)

Условия задачи: требуется найти оптимальный план перевозок грузов с трех станций отправления (А1, А2, А3) до 9 станций назначения (В4-12), т.е. такой план, для которого суммарная перевозочная работа (в т-км) была бы минимальной.

Исходные данные

Станции отправления

Станции назначения

А1

А2

А3

В4

В5

В6

В7

В8

В9

В10

В11

В12

125

200

175

40

45

50

55

65

60

75

70

40

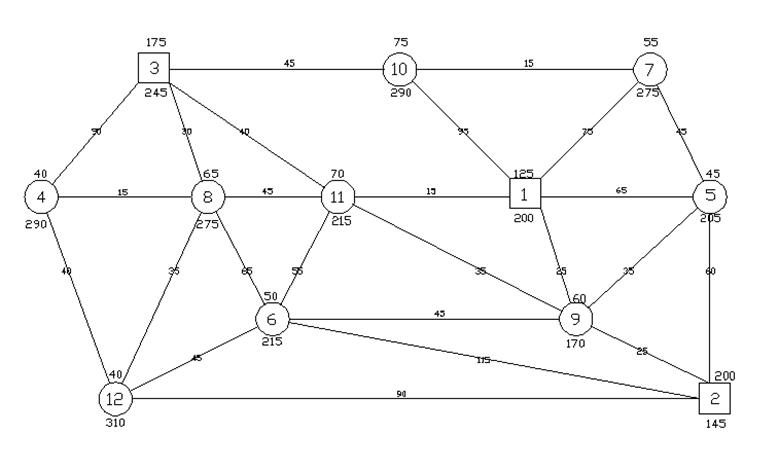
Рисунок 5.1 – Исходный железнодорожный полигон

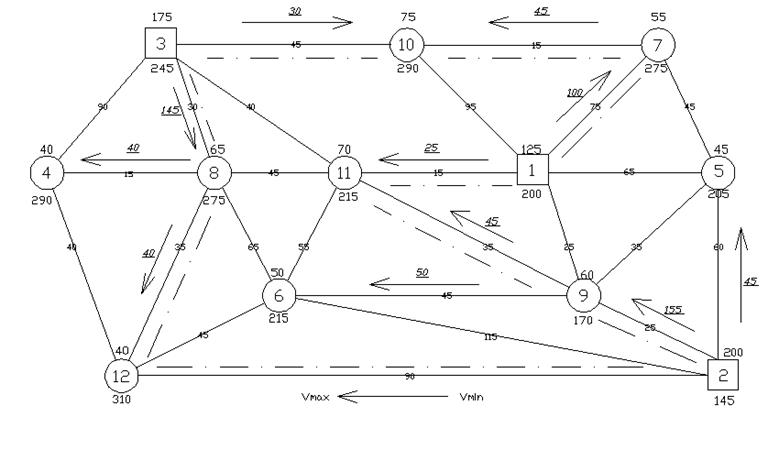
Рисунок 5.2 – Исходный вариант плана перевозок и направление его улучшения

Скачать файл