Определение оптимальной очередности возведения объектов (захваток), обеспечивающих минимальную продолжительность строительства при условии непрерывного использования ресурсов методом «ветвей и границ»

Задача №5

ИСХОДНЫЕ ДАННЫЕ:

-  количество захваток – m = 4;

-  количество процессов (бригад) – n = 4;

-  ритмы процессов по захваткам:

ОПРЕДЕЛИТЬ: оптимальную очередность возведения объектов (захваток), обеспечивающую минимальную продолжительность строительства при условии непрерывного использования ресурсов методом «ветвей и границ» (способ В. А. Афанасьева и В. З. Величкина).

РЕШЕНИЕ

При организации неритмичных потоков особое значение придают нахождению оптимальной очередности возведения объектов (захваток), обеспечивающей минимальный срок строительства.

Метод «ветвей и границ» устанавливает предельно возможный минимум продолжительности потока и находит рациональную очередность возведения объектов (захваток), приближающую поток к этому минимуму.

Алгоритм поиска оптимальной очередности возведения объектов (захваток), обеспечивающей минимальную продолжительность потока с непрерывным использованием ресурсов, состоит из пяти этапов:

Этап 1 – составляем исходную матрицу и выполняем расчет параметров потока:

НОМЕРА ЗАХВАТОК	РИТМЫ ПРОЦЕССОВ
	А		Б		В		Г
I	2		5		6		1
II	1		3		4		2
III	4		2		1		3
IV	3		1		2		5
		2		5		9

Т = S t_ин ^{i – (i+1)} + t_n = 2 + 5 + 9 + 11 = 27 дней.

Этап 2 – на основе исходной матрицы составляем парные матрицы (для каждой пары смежных процессов) и оптимизируем их по методу С. М. Джонсона.

Оптимизация по С. М. Джонсону заключается в том, что в парной матрице находят минимальное значение частного ритма. Если это значение относится к первому процессу, то данную строку (объект) в формируемой оптимизированной матрице переносят на первое место; если же это значение относят ко второму процессу, то данную строку (объект) переносят на последнее место в формируемой оптимальной парной матрице. Строка, перенесенная в формируемую оптимизированную матрицу, из дальнейшего рассмотрения исключается. Далее, среди оставшихся значений вновь находят минимальное значение ритма и шаг этот повторяют, заполняя строки (ближайшие к первой или последней) пока не заполнится вся формируемая парная матрица. 

ОПТИМИЗИРОВАННЫЕ ПАРНЫЕ МАТРИЦЫ

	А		Б				Б		В				В		Г
II	1		3			IV	1		2			III	1		3
I	2		5			II	3		4			IV	2		5
III	4		2			I	5		6			II	4		2
IV	3		1			III	2		1			I	6		1
		1						3						3

С помощью оптимальных парных матриц определяем предельно возможный минимум продолжительности потока (ПВМП) как сумму интервалов времени между началами смежных процессов плюс продолжительность последнего процесса:

ПМВП = S t_ин ^{i – (i+1)} + t_n = 1 + 3 + 3 + 1 1 = 18 дней.

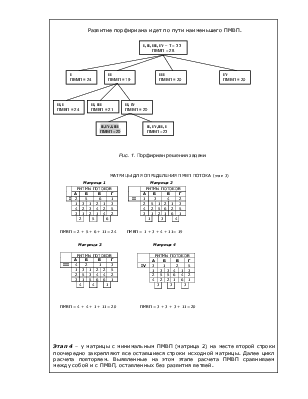
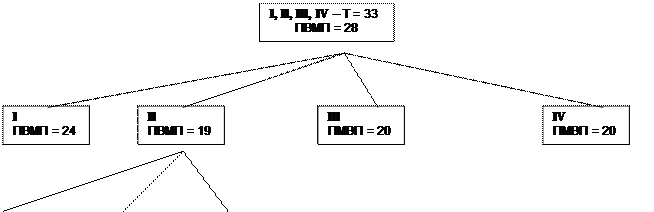
Этап 3 – строим порфириан (дерево цели) с последовательным закреплением в первой строке каждого варианта номера объекта (захватки), с которого будет начинаться поток по этому варианту; во второй строке записываем ПМВП.

Развитие порфириана идет по пути наименьшего ПМВП.  

 

II, IV ПМВП = 20

                                                                         

	II, I ПМВП = 24

II,IV,I,III ПМВП =20 393933939393439

II, IV,III, I ПМВП =23 393933939393439

                                     

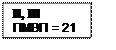
Рис. 1. Порфириан решения задачи

МАТРИЦЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПМВП ПОТОКА (этап 3)

                       Матрица 1                                  Матрица 2

	РИТМЫ ПОТОКОВ
	А		Б				В				Г
I	2		5				6				1
	1		3		1		2		1		3
	4		2		3		4		2		5
	3		1		2		1		4		2
		2				5				6