Федеральное агентство по образованию
Государственное образовательное учреждение
Высшего Профессионального образования
«Государственный университет цветных металлов и золота»
Кафедра «Автоматизации
производственных процессов»
Лабораторная работа №2п
«Алгебраическое суммирование на дросселях УСЭППА»
по курсу: «Элементы систем автоматики» для студентов специальности 220301
Рассмотрено на заседании
кафедры АПП ___________
(Протокол № ______).
Красноярск 2006
Лабораторная работа №2п (4часа)
Алгебраическое суммирование на дросселях УСЭППА
Цель работы: ознакомление с устройством, принципом действия, характеристиками дроссельного сумматора, реализация на его базе простейших алгебраических операций, снятие статических характеристик.
1.Теоретическая часть
Суммирование пневматических сигналов можно осуществить на дроссельном сумматоре. Простейшим дроссельным сумматором является сумматор на два сигнала, представляющий собой пневматическую камеру, к которой через дроссели подводятся слагаемые давления
(рис 1).
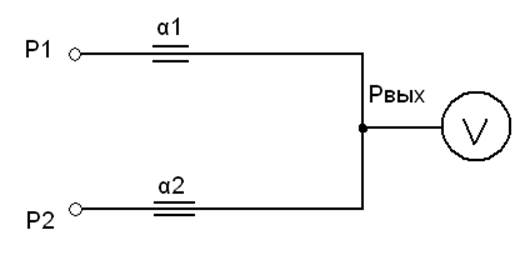
Рис.1. Схема сумматора на два сигнала.
Допустим, что воздух в камеру поступает через дроссель α1, а вытекает через α2. Тогда, полагая, что расход воздуха через дросселирующее сопротивление является линейной функцией от перепада давлений, получаем
q1=α(Р1-Рвых); q2+ α(Pвых-Р2), (1)
где q1, q2 - расход воздуха соответственно через первое и второе дросселирующие сопротивления; α1, α2 – проводимости первого и второго дросселя.
В статике из условия равенства расхода воздуха, поступающего в камеру и вытекающего из неё (q1= q2), получаем
α1(Р1- Рвых) = α2(Рвых- Р2) (2)
Решив это уравнение относительно Рвых
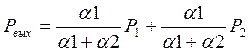(3)
или
обозначив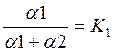 
, 
,
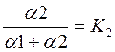получим
Рвых = К1P1 + К2 Р2. (4)
В уравнении (4) О К1 < 1, О < К2 < 1, К1 + К2 = 1.
Все приведенные выше рассуждения можно перенести на
сумматор
с дросселями. Тогда аналогично выражению
(4) можно записать
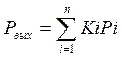
(5)
Где
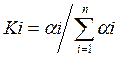и, следовательно, 0 < Ki < 1,
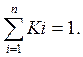
В частном случае, если α1 = α2 = … = αi= …αn,
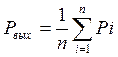
т.е. на выходе сумматора создается давление, равное среднему арифметическому от входных давлений. Однако условие (6) ограничивает возможность рассматриваемого сумматора. С его помощью нельзя производить обычное сложение, так как Ki< 1, и вычитание, так как Ki > 0 . Несмотря на это, такие сумматоры вследствие своей простоты широко применяются в устройствах пневмоавтоматики для решения задач соответствующих условию (6).
Уравнение (5), показывающее возможность суммирования давлений на дросселирующих сопротивлениях, записано в предположении, что весовых секундные расходы через них являются линейной функцией перепада. Однако системы пневмоавтоматики в связи со сжимаемостью воздуха не располагают дросселями, полностью отвечающими этому требованию, что и предопределяет основную погрешность такого рода сумматоров. Поэтому целесообразно выполнять операцию суммирования на низких давлениях порядка 1 кПа с последующим усилением выходного сигнала.
Описанный сумматор позволяет суммировать неограниченное число слагаемых, не имеет механических перемещений и, в связи с этим, зоны нечувствительности, обычно обуславливаемой трением. В конструктивном отношении он чрезвычайно прост.
В качестве сопротивлений, входящих в сумматор, можно использовать как постоянные, так и переменные сопротивления. На рис.2 представлены схемы трех разновидностей сумматоров на два сигнала:
а) –постоянное-постоянное; б) – регулируемое-регулируемое и
в) –постоянное-регулируемое сопротивление. Последний сумматор получил наиболее широкое распространение и, поэтому, этот типовой узел выполнен как единое устройство.
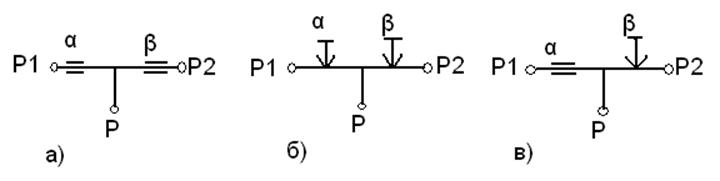
Рис.2. Схемы дроссельных сумматоров: а) + постоянное-постоянное;
б) + переменно-переменное; в) - постоянное-переменное сопротивления.
1. Порядок выполнения работы
1.Установить на ПУЛС съемную панель № 8.
2.Собрать схему дроссельного сумматора (Рис.3).
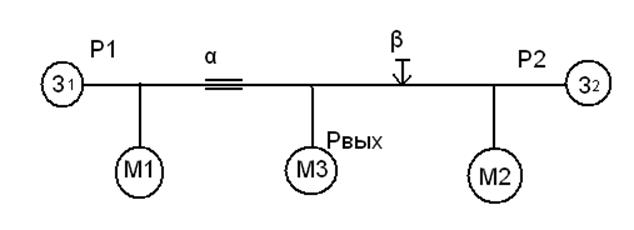
Рис.3. Схема дроссельного сумматора постоянное-переменное
сопротивление: З1, З2 – задатчики давлений Р1 и Р2;
М1, М2, М3 – манометры
Для этого подать давления Р1 и Р2 от задатчиков З1 и З2, расположенных на лицевой панели на входы дроссельного сумматора, и одновременно через тройники на контрольные манометры М1 и М2. Выходной сигнал дроссельного сумматора Рвых подать на манометр М3.
3. При Р2=0 и максимальном открытии переменного дросселя β, изменяя давление Р1 с помощью задатчика З1, снять характеристику
Рвых = f(Р1).
4.Снять ту же характеристику при других положениях дросселя β
вплоть до его полного закрытия.
5.Определить аналогичные характеристики дроссельного сумматора при других значениях давления Р2 (по указанию преподавателя).
6.Построить характеристики дроссельного сумматора, проанализировать и сделать выводы.
3.Содержание отчета
Отчет должен содержать наименование и цель работы, теоретическую часть, схемы дроссельных сумматоров, протоколы по снятию статических характеристик и их графики, выводы по работе.
2. Контрольные вопросы
1.Объясните устройство и принцип работы постоянного и переменного дросселей.
2.Какая операция выполняется на дроссельном сумматоре?
3.Составьте выражение, связывающее входные Р1 и Р2, и выходное давления сумматора.
4.Объясните нелинейность статической характеристики дроссельного сумматора.
5.Почему коэффициент передачи дроссельного сумматора не может превышать единицы?
Составил: доцент кафедры АПП Тихонов В.П.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
