Типовые алгоритмы цифровых регуляторов. Расчет оптимальных настроек цифровых регуляторов

Лекция 6.

1. Типовые алгоритмы цифровых регуляторов.

2. Расчет оптимальных настроек цифровых
     регуляторов .

3. Дискретный и  непрерывный методы.

Синтез типовых алгоритмов цифровых регуляторов

При малом периоде квантования t_s цифровые регуляторы можно заменить их непрерывными аналогами и вести расчет параметров настроек обычными методами. ТАУ показывает, что в этом случае АЦП - дельта-импульсный модулятор - можно заменить  непрерывным  безинерционным звеном с  К_п = 1/ t_s

ПФ непрерывного регулятора, эквивалентного дискретному регулятору
с ПФ W_р(z),  имеет вид:

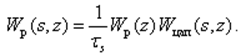
Задавшись желаемой ПФ непрерывного регулятора W_р.ж(s) » W_р.ж(s,z),можно найти ПФ цифрового регулятора

Если ЦАП использует фиксатор нулевого порядка ZOH с Z-ПФ и S-ПФ

то ПФ регулятора равна:

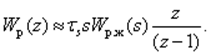                                                 (19)

И-алгоритм

Непрерывный алгоритм его работы точно  реализуется цифровым регулятором, так как при

                                                  (20)

П-алгоритм

Желаемая ПФ П-регулятора

ДПФ П-регулятора с учетом (19)

Так как ПФ цифровых дифференциаторов обратны ПФ цифровых интеграторов, с учетом формул (16) и (17) перехода к ДПФ (от sк z) для П-регулятора имеем:

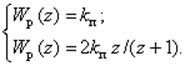                                             (21)

Из (19)  непрерывные ПФ для них

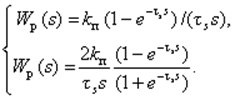                                      (22)

ПИ-алгоритм

Реализуется суммированием ДПФ цифровых И- и П-регуляторов или

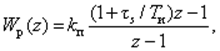                                                 (23)

где  Т_и = k_п / k_и.

Непрерывная  ПФ цифровых  ПИ -регуляторов равна

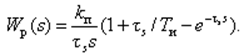                                             (24)

ПИД-алгоритм

Желаемая  ПФ регулятора такова

где k_д = k_п Т_д.      

С учетом (19) ДПФ регулятора равна

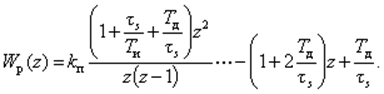                               (25)

Непрерывная  ПФ цифрового ПИД-регулятора равна

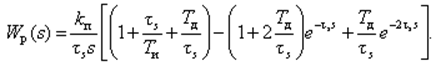                               (26)

Расчет оптимальных настроек цифровых регуляторов

В режиме получения достаточно полной информации об изменении регулируемой величины расчет  может осуществляться методами как теории дискретных систем, так и теории непрерывных систем.

Обычно используют графический  метод определения оптимальных параметров настройки регуляторов.

Порядок построения обычный: вначале строят АФХ объекта, а затем по ней строят АФХ разомкнутой СУ. При этом учитывают модуль составляющих (П-, И-, Д-) закона управления и угол их поворота относительно исходного вектора АФХ объекта.

Дискретный метод

1. Задаваясь значениями частоты  ω строят АФХ дискретного ОУ по его непрерывной ПФ.

2. По ДПФ регулятора находят выражения для составляющих закона регулирования, по ним вычисляют значения АФХ регулятора для частот ω .

3. Прибавляя вектора составляющих закона регулирования, строят АФХ разомкнутой СУ для частот ω .

Согласно (23), АФХ ПИ-регулятора

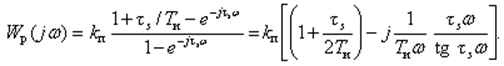                     (27)

В существенном для расчета диапазоне частот от 0 до 3/4 π выражение (27) можно упростить:

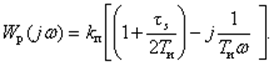                                         (28)

Отличие от  аналогового ПИ-регулятора – в увеличении модуля П-составляющей на t_s / 2T_и .

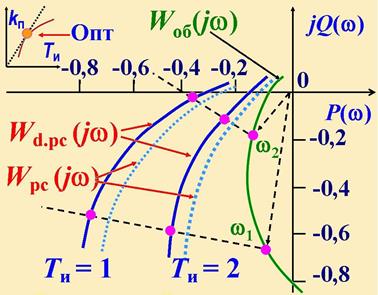
Таким образом, цифровой регулятор обеспечивает меньший запас устойчивости, чем непрерывный.

Дальнейший расчет оптимальных параметров настройки аналогичен расчету непрерывных регуляторов:

   - проводят луч под углом γ (по М);

   - строят окружности и находят r , k_п;

   - для нескольких k_п, Т_и, а затем и Т_д находят оптимальные параметры настройки регулятора.

Непрерывный метод

В нем вместо ДПФ цифрового регулятора Wр(z)используется ПФ эквивалентного непрерывного регулятора W_р(s).

Для ПИ-регулятора согласно формул (23) и (19) ПФ имеет вид:

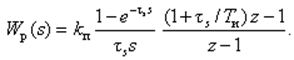
После преобразований имеем

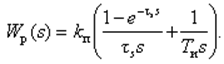
Тогда АФХ непрерывного эквивалентного ПИ-регулятора

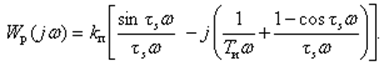                                 (29)

Таким образом, отличие от расчета аналогового ПИ-регулятора состоит в том, что длина отрезков П- и И- составляющих АФХ разомкнутой системы определяют по более сложному закону:

П- составляющая     

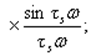
И- составляющая

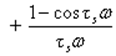
Расчет оптимальных параметров настройки цифровых регуляторов методами теории дискретных систем имеет более универсальный характер и может применяться всегда.

Расчет методами теории непрерывных систем возможен лишь при отсутствии пульсаций квантования, т.е. лишь при большой частоте квантования (малом t_s), но он более прост.