Прохождение сигналов через простейшие RC-цепи (лабораторная работа), страница 2

Дифференцирующая RC-цепь. Схема цепи приведена на рисунке 4.2.

 

Коэффициент передачи такой цепи:

                                            (4.6)

Частотный коэффициент передачи

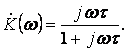                                                                               (4.7)

Из этого выражения видно, что такая цепь пропускает высокие частоты, задерживая низкие, т.е. является фильтром верхних частот (ФВЧ). Частота среза фильтра, на которой модуль коэффициента передачи составляет  от максимального значения, определяется выражением (4.3).

Согласно свойствам преобразования Фурье, при дифференцировании его спектр умножается на . Учитывая это, из (4.7) находим, что цепь будет дифференцирующей, если , где  – верхняя граничная частота спектра сигнала.

Импульсная характеристика дифференцирующей цепи

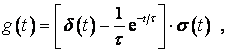                                                           (4.8)

где – дельта-функция.

Переходная характеристика дифференцирующей цепи

                                                                            (4.9)

Для анализа прохождения сигнала через линейную цепь с постоянными параметрами применяют спектральный, операторный или временной (интеграла наложения) методы.

Спектральный метод позволяет отыскать спектральную плотность выходного сигнала  по известным частотному коэффициенту передачи цепи  и спектральной плотности входного сигнала :

.                                                                 (4.10)

Для нахождения выходного сигнала  необходимо воспользоваться обратным преобразованием Фурье.

Операторный метод позволяет отыскать изображение выходного сигнала  по известным коэффициенту передачи цепи  и изображению входного сигнала :

.                                                                 (4.11)

В соответствии с методом интеграла наложения сигнал на выходе цепи равен свертке входного сигнала и импульсной характеристики цепи:

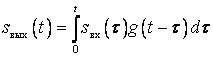.                                                           (4.12)

Рассмотрим прохождение прямоугольного видеоимпульса, приведенного на рисунке 4.3, через интегрирующую RC-цепь.