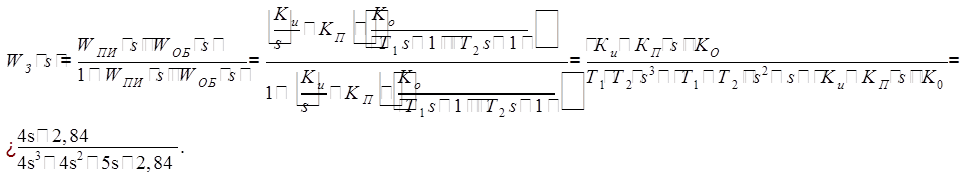
6) Проверим экспериментально выполнение условий устойчивости для И и ПИ-регуляторов при Ku взятом из области устойчивости.
а) Для И- регулятора – рисунок 2. Возьмем Ku =0,1
б) Для ПИ-регулятора – рисунок 3. Возьмем Ku =1
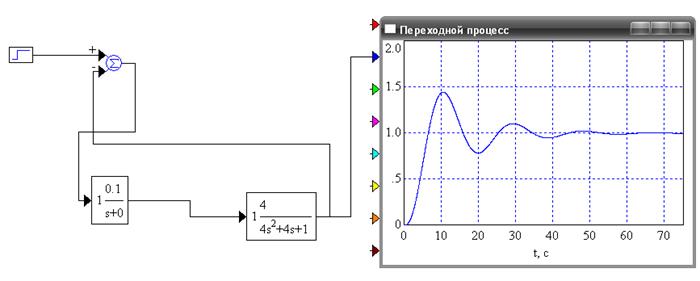
Рисунок 2 - Переходной процесс для И -регулятора при Ки, взятом из области устойчивости
Величина перерегулирования для процесса будет:
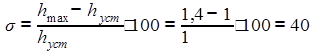 .
.
Время
переходного процесса: ![]()
Вывод: система при Ки=0,1
устойчива, т. к. переходной процесс колебательный затухающий, а также она
имеет удовлетворительное качество процесса регулирования, т. к. ![]() .
.
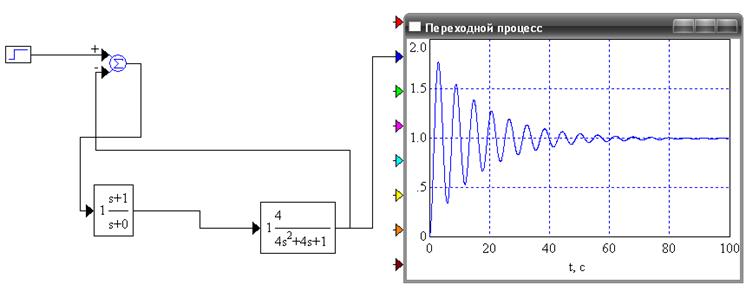
Рисунок 3 - Переходной процесс для ПИ-регулятора при Ки, взятом из области устойчивости
Величина перерегулирования для процесса будет:
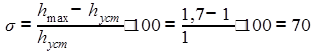 .
.
Время
переходного процесса: ![]()
Вывод: система при Ки=1
устойчива, т. к. переходной процесс колебательный, плохо затухающий, склонный к
длительным колебаниям, а также система имеет неудовлетворительное качество
процесса регулирования, т. к. ![]() .
.
7) Проверим экспериментально выполнение условий устойчивости для И и ПИ-регуляторов при Ku = Kuопт.
а) И-регулятор при Ки опт =0,084 - рисунок 4.
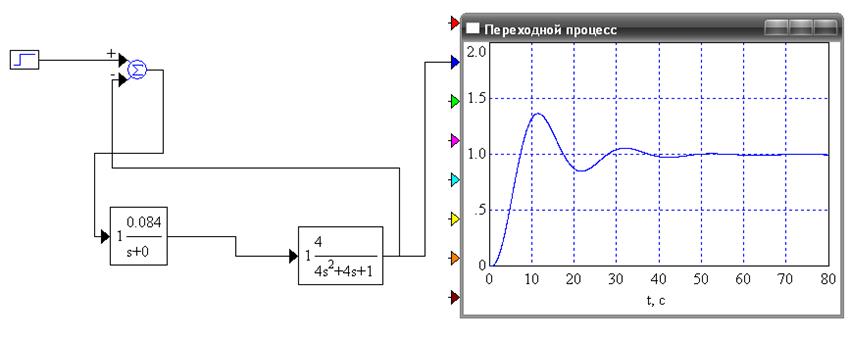
Рисунок 4 - Переходной процесс для И-регулятора при Ки опт=0,084
Величина перерегулирования:
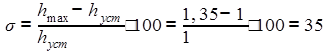 .
.
Время
переходного процесса: ![]()
Вывод: система при Ки=0,084
устойчива, т. к. переходной процесс колебательный затухающий, а также она
имеет удовлетворительное качество процесса регулирования, т. к. ![]() .
.
б) Пи-регулятор при Ки опт =0,71 - рисунок 5.
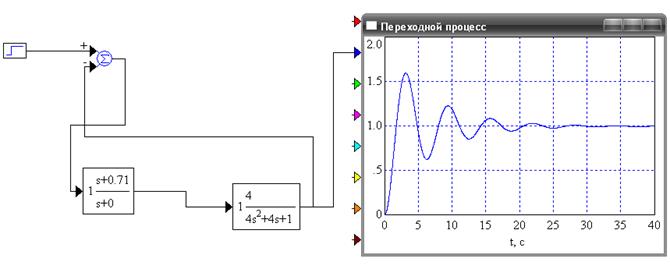
Рисунок 5 - Переходной процесс для ПИ-регулятора при Ки опт=0,71
Величина перерегулирования:
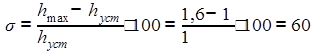 .
.
Время
переходного процесса: ![]()
Вывод: система при Ки
опт =0,71 устойчива, переходной процесс колебательный, плохо затухающий,
склонный к длительным колебаниям, а также система имеет неудовлетворительное
качество процесса регулирования, т. к. ![]() .
.
8) Для САР с И и
ПИ-регулятором экспериментально исследуем переходной процесс при различных
значениях Ku. (при ![]() и
и ![]() )
)
а)
И-регулятор при ![]()
![]() - рисунок 6.
- рисунок 6.
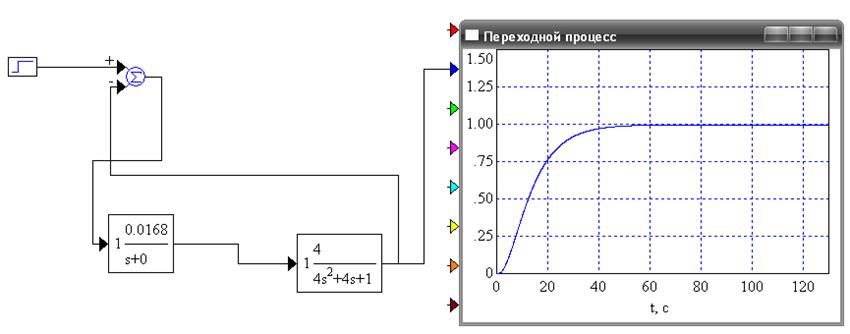
Рисунок 6 - Переходной процесс для И-регулятора при Ки=0,0168
Величина перерегулирования:
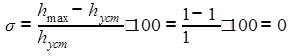 .
.
Время
переходного процесса: ![]()
Вывод: система при Ки=0,0168
устойчива, т. к. переходной процесс монотонный и ![]() Перерегулирование
равно 0 %.
Перерегулирование
равно 0 %.
б)
И-регулятор при ![]()
![]() - рисунок 7.
- рисунок 7.
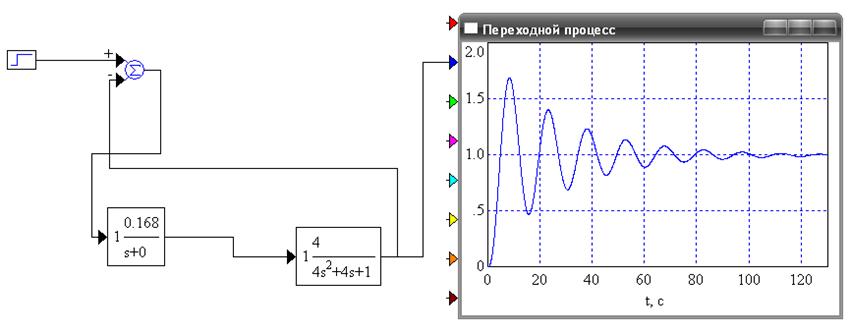
Рисунок 7 - Переходной процесс для И-регулятора при Ки=0,168
Величина перерегулирования:
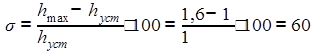
Время
переходного процесса: ![]()
Вывод: система при Ки=0,168
устойчива, переходной процесс колебательный, плохо затухающий, склонный к
длительным колебаниям, а также система имеет неудовлетворительное качество
процесса регулирования, т. к. ![]() .
.
в) Пи-регулятор при![]()
![]() - рисунок 8.
- рисунок 8.
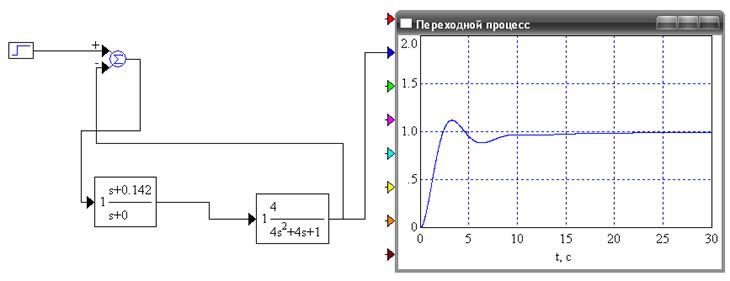
Рисунок 8 - Переходной процесс для ПИ-регулятора при Ки=0,142
.
Величина перерегулирования:
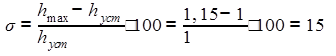
Время
переходного процесса: ![]()
Вывод: система при Ки=0,142
устойчива, т. к. переходной процесс колебательный затухающий, а также она имеет
удовлетворительное качество процесса регулирования, т. к. ![]() .
.
г)
Пи-регулятор при![]()
![]() - рисунок 9.
- рисунок 9.
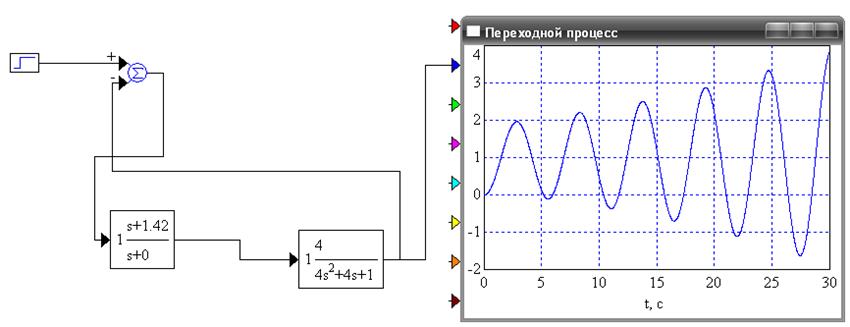
Рисунок 9 - Переходной процесс для ПИ-регулятора при Ки=1,42
Вывод: система при Ки=1,42 неустойчива, т. к.
переходной процесс расходящийся, ![]() =1,42 выходит за пределы области устойчивости,
=1,42 выходит за пределы области устойчивости,
т. е. можно сделать вывод, что “система пошла в разнос”.
9) Проверяем систему на устойчивость и строим график расположения корней (рисунок 10) и годограф Найквиста (рисунок 11). Находим критический коэффициент усиления системы.
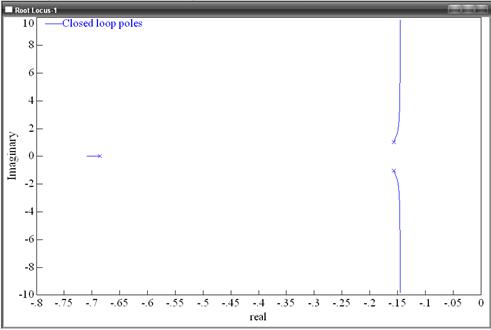
Рисунок 10 - График расположение корней.
Вывод: система устойчива, так корни характеристического уравнения лежат в левой полуплоскости комплексной плоскости.
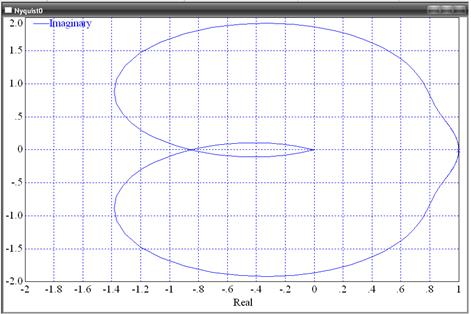
Рисунок 11 - Годограф Найквиста.
Вывод:
замкнутая система устойчива, т. к. АФЧХ разомкнутой системы при изменении
частоты ![]() не
охватывает точку с координатами
не
охватывает точку с координатами ![]() .
.
10) Построим годограф Михайлова – рисунок 12.
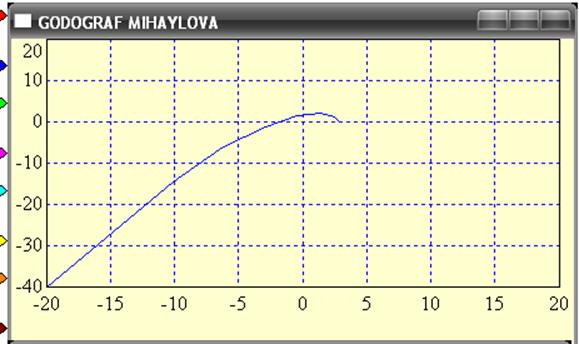
Рисунок 12 - Годограф Михайлова.
Вывод: замкнутая система устойчива, т. к. годограф Михайлова, начинаясь на положительной вещественной оси последовательно проходит 3 квадранта в положительном направлении.
Запас
устойчивости: ![]()
11) Исследуем на устойчивость систему с помощью критерия устойчивости Гурвица.
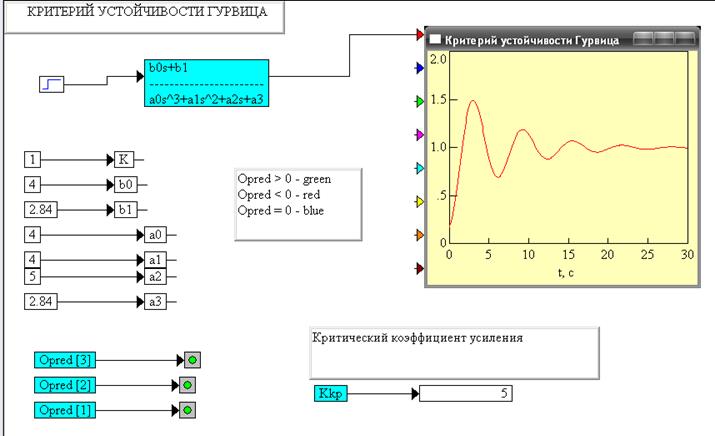
Вывод: система устойчива, т.к. главный определитель Гурвица и все его диагональные миноры положительны. (на графике они обозначены зеленым цветом).
12)
Построим график зависимости ![]() в Mathcad для П-регулятора – рисунок 13.
в Mathcad для П-регулятора – рисунок 13.
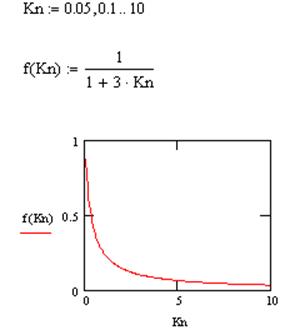
Рисунок 13 - График зависимости ![]() для
П-регулятора
для
П-регулятора
Вывод: с увеличением Kп
установившаяся ошибка ![]() стремится к нулю
стремится к нулю
13) Для САР с И и
ПИ-регулятором построим в Mathcad графики зависимости ![]() .
.
а) И-регулятор – рисунок 14.
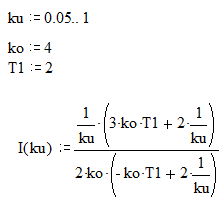
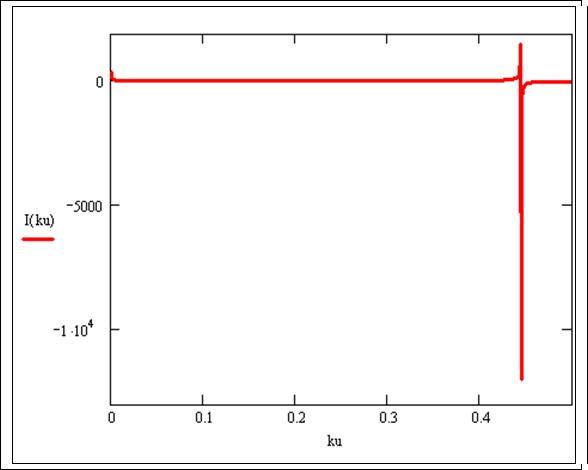
Рисунок 14 - График зависимости ![]() для И-регулятора.
для И-регулятора.
б) ПИ-регулятор – рисунок 15.
ku := 0.001,0.1..1.78

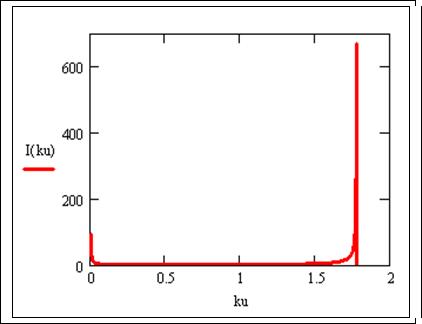
Рисунок 15 - График зависимости ![]() для ПИ-регулятора.
для ПИ-регулятора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.