



Федеральное агентство по образованию
Институт цветных металлов и золота ФГОУ ВПО
Сибирский Федеральный Университет
Факульет ФМ
Кафедра АПП
Специальность Автоматизация технологических процессов и производств
Группа АМЦ 03-2
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1
«Изучение пакета Control System Toolbox системы MATLAB 6
и его применения для расчета систем управления»
Вариант 16
Преподаватель А.А. Буралков
Разработал студент А.А. Харченко
Красноярск, 2007 г.
Ход работы
1)
>> s=tf('s'); h1=2.3/((8*s+1)*(2.7*s+1))
Transfer function:
2.3
-------------------------
21.6 s^2 + 10.7 s + 1
>> h2=tf(2.3,[21.6 10.7 1],'inputdelay',1.5)
Transfer function:
2.3
exp(-1.5*s) * -------------------------
21.6 s^2 + 10.7 s + 1
>> zh1=zpk(h1)
Zero/pole/gain:
0.10648
-------------------------
(s+0.3704) (s+0.125)
>> zh2=zpk(h2)
Zero/pole/gain:
0.10648
exp(-1.5*s) * -------------------------
(s+0.3704) (s+0.125)
>> ssh1=ss(h1)
a =
x1 x2
x1 -0.4954 -0.09259
x2 0.5 0
b =
u1
x1 0.5
x2 0
c =
x1 x2
y1 0 0.4259
d =
u1
y1 0
Continuous-time model.
>> ssh2=ss(h2)
a =
x1 x2
x1 -0.4954 -0.09259
x2 0.5 0
b =
u1
x1 0.5
x2 0
c =
x1 x2
y1 0 0.4259
d =
u1
y1 0
Input delays (listed by channel): 1.5
Continuous-time model.
>>conv([8 1],[2.7 1])
ans =
21.6000 10.7000 1.0000
2)
>> step(h1,h2)
>> step(zh1,zh2)
>> step(ssh1,ssh2)
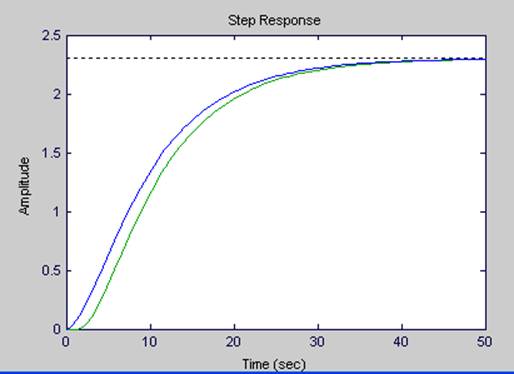
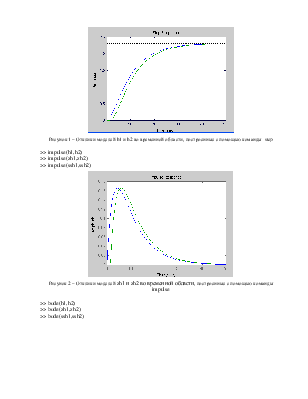
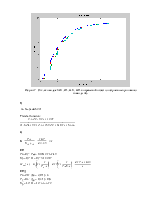
Рисунок 1 – Отклики моделей h1 и h2 во временной области, построенные с помощью команды step
>> impulse(h1,h2)
>> impulse(zh1,zh2)
>> impulse(ssh1,ssh2)
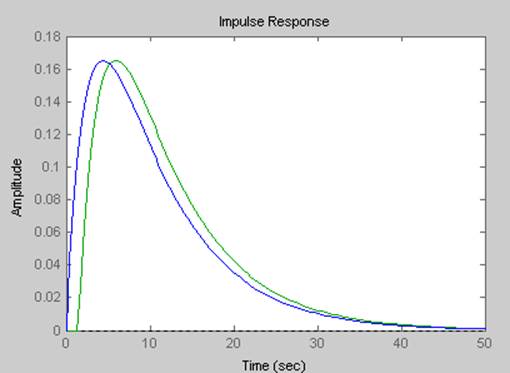
Рисунок 2 – Отклики моделей zh1 и zh2 во временной области, построенные с помощью команды impulse
>> bode(h1,h2)
>> bode(zh1,zh2)
>> bode(ssh1,ssh2)
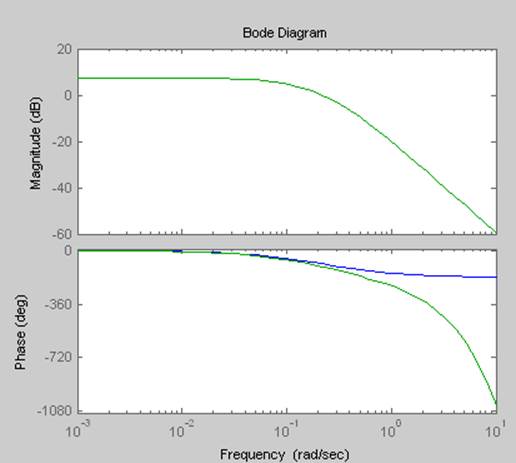
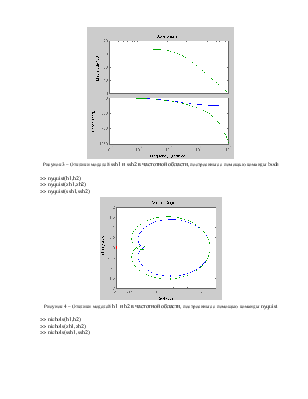
Рисунок 3 – Отклики моделей ssh1 и ssh2 в частотной области, построенные с помощью команды bode
>> nyquist(h1,h2)
>> nyquist(zh1,zh2)
>> nyquist(ssh1,ssh2)
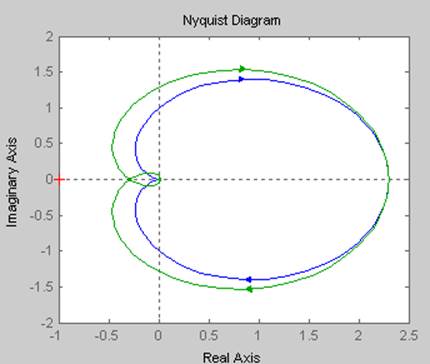
Рисунок 4 – Отклики моделей h1 и h2 в частотной области, построенные с помощью команды nyquist
>> nichols(h1,h2)
>> nichols(zh1,zh2)
>> nichols(ssh1,ssh2)
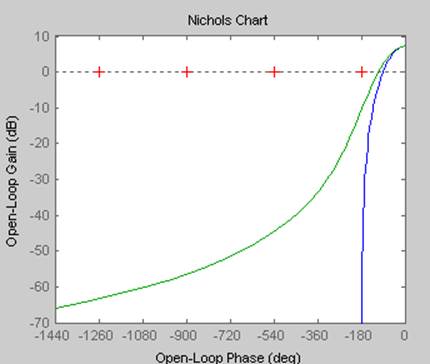
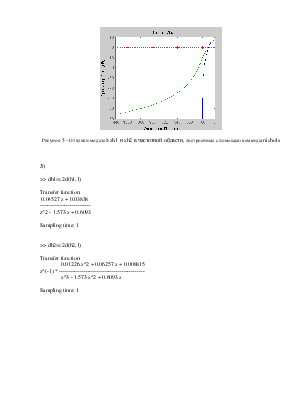
Рисунок 5 – Отклики моделей zh1 и zh2 в частотной области, построенные с помощью команды nichols
3)
>> dh1=c2d(h1,1)
Transfer function:
0.04527 z + 0.03838
---------------------------
z^2 - 1.573 z + 0.6093
Sampling time: 1
>> dh2=c2d(h2,1)
Transfer function:
0.01226 z^2 + 0.06257 z + 0.008815
z^(-1) * ---------------------------------------------
z^3 - 1.573 z^2 + 0.6093 z
Sampling time: 1
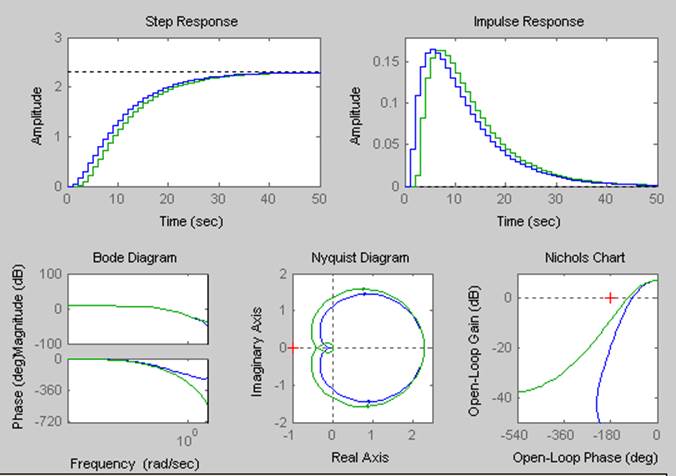
Рисунок 6 – Отклики моделей dh1 и dh2 в частотной и временной областях
4)
>> ddh1=d2d(dh1,0.5)
Transfer function:
0.01226 z + 0.01129
--------------------------
z^2 - 1.77 z + 0.7806
Sampling time: 0.5
>> ddh2=c2d(h2,0.5)
Transfer function:
0.01226 z + 0.01129
z^(-3) * --------------------------
z^2 - 1.77 z + 0.7806
Sampling time: 0.5
>> step(dh1,dh2,ddh1,ddh2)
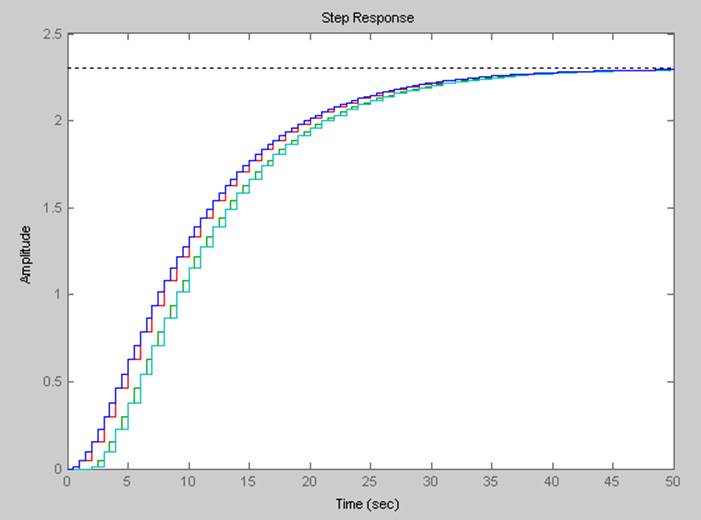
Рисунок 7 – Отклики моделей dh1, dh2, ddh1, ddh2 во временной области, построенные при помощи команды step
5)
>> h3=pade(h2,2)
Transfer function:
2.3 s^2 - 9.2 s + 12.27
----------------------------------------------------------
21.6 s^4 + 97.1 s^3 + 159 s^2 + 61.07 s + 5.333
6)
В =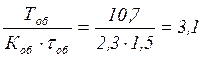
ПИ
Ти =0,7· Тоб = 0,7(8+2,7)=7,49
Кр=0,7· В =0,7·3,1=2,17
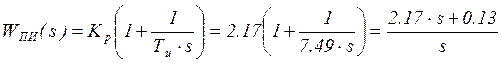
ПИД
Ти =2,0· tоб = 2,0·1,5=3
Тд =0,4· tоб = 0,4·1,5=0,6
Кр=1,2· В =1,2·3,1=3,72
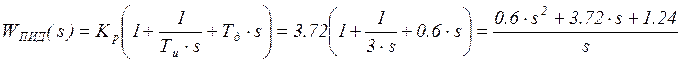
>> s=tf('s'),g1=tf(2.17*(1+1/(7.49*s)))
Transfer function:
s
Transfer function:
16.25 s + 2.17
--------------
7.49 s
>> s=tf('s'),g2=tf(3.72*(1+1/(3*s)+0.6*s))
Transfer function:
s
Transfer function:
6.696 s^2 + 11.16 s + 3.72
--------------------------
3 s
7)
>> oh1=h1*g1
Transfer function:
37.38 s + 4.991
------------------------------
161.8 s^3 + 80.14 s^2 + 7.49 s
>> oh2=h3*g2
Transfer function:
15.4 s^4 - 35.94 s^3 - 11.98 s^2 + 102.7 s + 45.63
--------------------------------------------------
64.8 s^5 + 291.3 s^4 + 477 s^3 + 183.2 s^2 + 16 s
8)
>> clh1=feedback(h1,g1,-1)
Transfer function:
17.23 s
---------------------------------------
161.8 s^3 + 80.14 s^2 + 44.87 s + 4.991
>> clh2=feedback(h3,g2,-1)
Transfer function:
6.9 s^3 - 27.6 s^2 + 36.8 s
--------------------------------------------------------------
64.8 s^5 + 306.7 s^4 + 441.1 s^3 + 171.2 s^2 + 118.7 s + 45.63
9)
>> zllh2=zpk(clh2)
Zero/pole/gain:
0.10648 s (s^2 - 4s + 5.333)
----------------------------------------------------------
(s+0.4356) (s^2 - 0.16s + 0.3024) (s^2 + 4.457s + 5.345)
10)
>> step(clh1,zllh2)
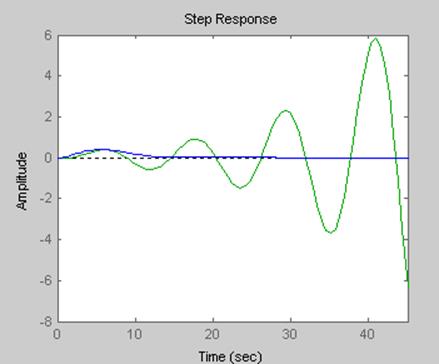
Рисунок 8 - Отклики моделей clh1 и zllh2 во временной области, построенные при помощи команды step
>> impulse(clh1,zllh2)
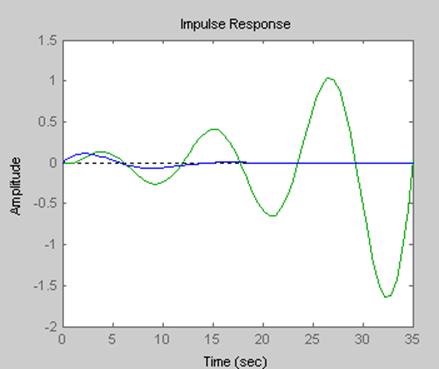
Рисунок 9 - Отклики моделей clh1 и zllh2 во временной области, построенные при помощи команды impulse
>> bode(clh1,zllh2)
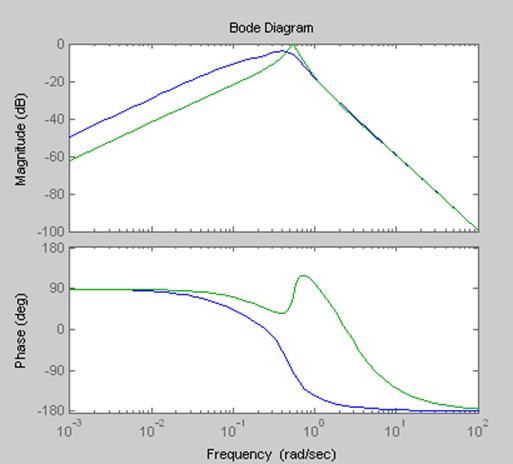
Рисунок 10 - Отклики моделей clh1 и zllh2 в частотной области, построенные при помощи команды bode
>> nyquist(clh1,zllh2)
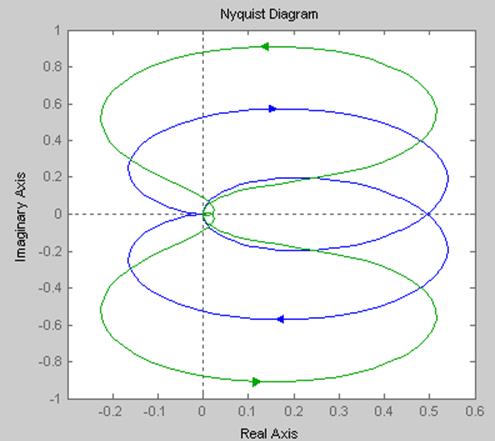
Рисунок 11 - Отклики моделей clh1 и zllh2 в частотной области, построенные при помощи команды nyquist
>> nichols(clh1,zllh2)
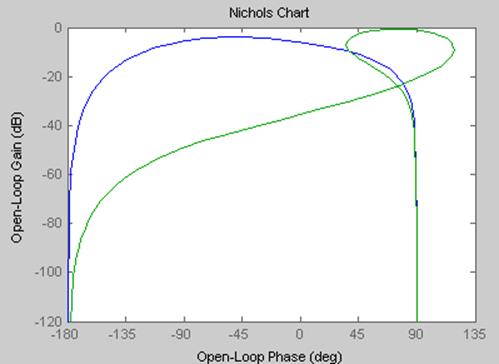
Рисунок 12 - Отклики моделей clh1 и zllh2 в частотной области, построенные при помощи команды nichols
Т.к. модель с запаздыванием zclh2 дает расходящийся переходной процесс, изменим настройки регулятора g2. Уменьшим величину Кр до значения 0.72. И получим новые характеристики.
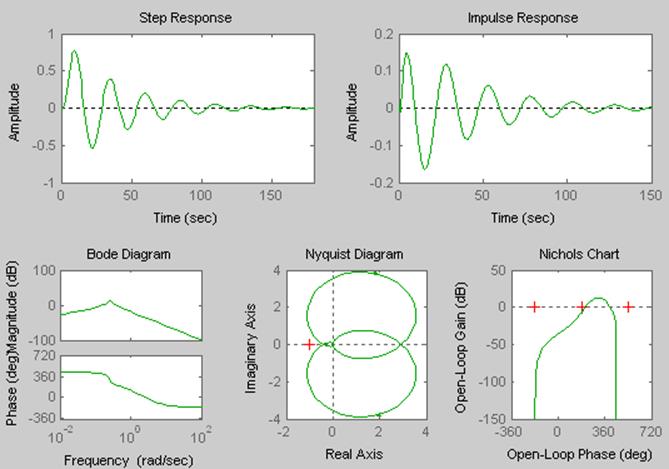
Рисунок 13 - Отклик модели zllh2 в частотной и временной областях
Изменив настройки регулятора, добились того, чтобы модель zllh2 давала сходящийся переходной процесс.
11)
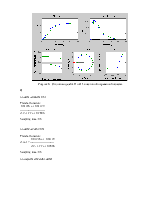
>> ltiview
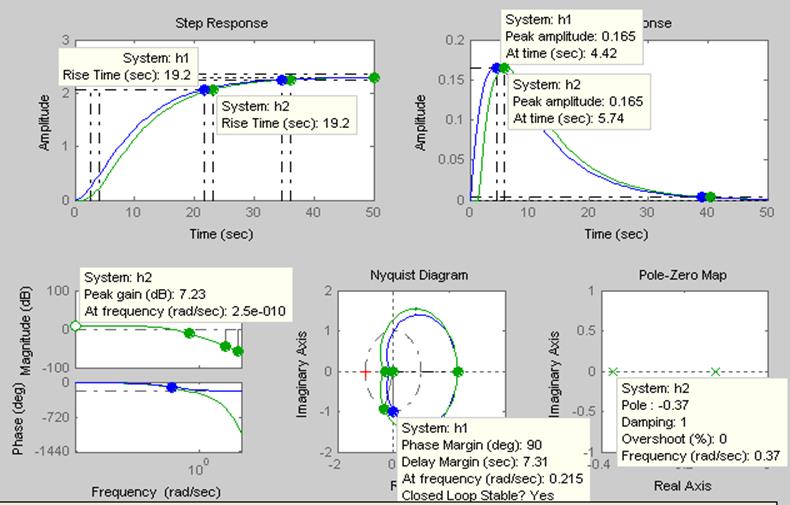
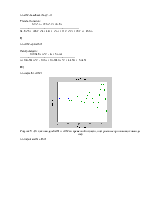
Рисунок 14 - Определение значений характерных точек моделей h1 и h2
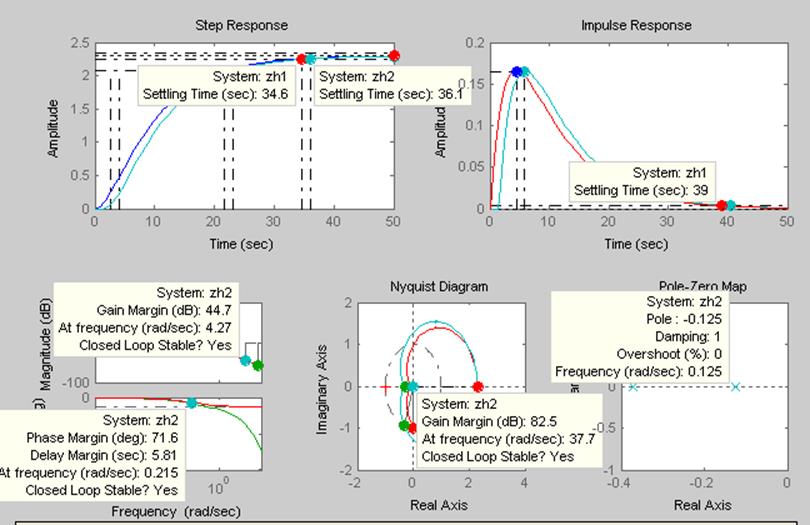
Рисунок 15 - Определение значений характерных точек моделей zh1 и zh2
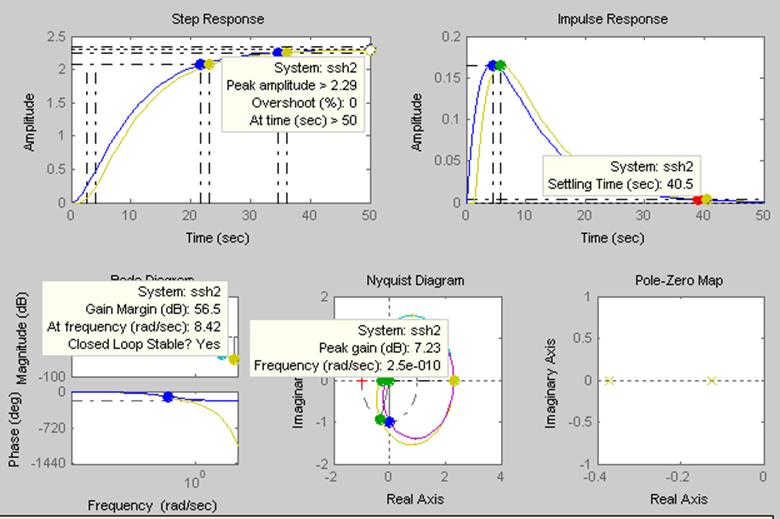
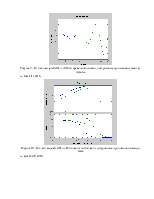
Рисунок 16 - Определение значений характерных точек моделей ssh1 и ssh2
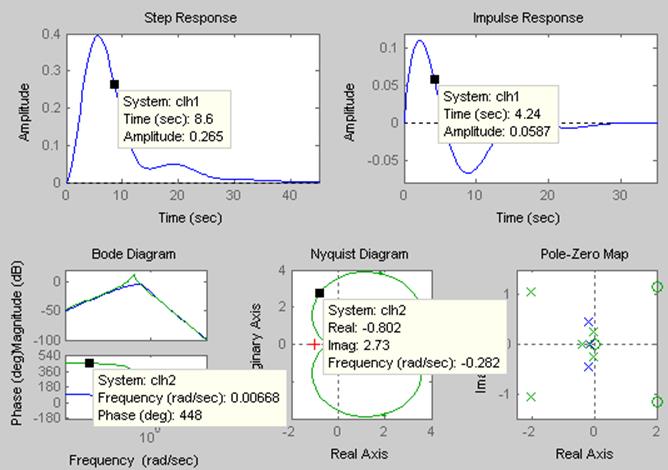
Рисунок 17 - Определение значений характерных точек моделей clh1 и clh2
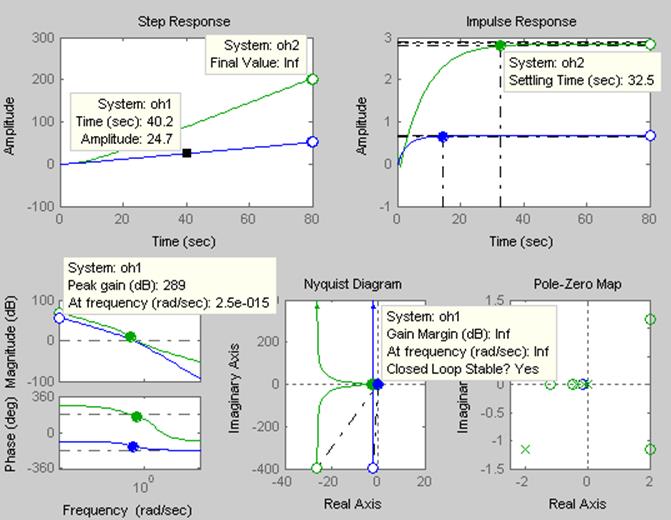
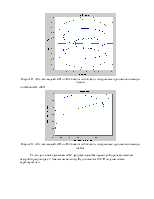
Рисунок 18 - Определение значений характерных точек моделей oh1 и oh2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.