Кинематический анализ плоского механизма

.Задание К.3. Кинематический анализ плоского механизма.

Найти для заданного положения механизма скорости и ускорения точек В и С, а так же угловую скорость и угловое ускорение звена, которому эти точки принадлежат.

Исходные данные:

АВ = 30, см

АС = 15, см

V_а = 10, см/с

а_а = 0, см/с²

Найти: V_в, V_с,,  а_в, а_с, - ?

Решение.

1). Анализ движения.

   На рисунке №1 изображен механизм состоящий из ползунов А и В к которым прикреплена линейка эллипсографа. Ползуны А и В перемещаются по взаимно перпендикулярным направляющим, со скоростью V_A и V_B совершают поступательное прямолинейное движение. Линейка эллипсографа АВ совершает плоское движение.

2). Определение м.ц.с.

      Для линейки АВ эллипсографа направление скоростей точек А и В известны. Восставляя к ним перпендикуляры, найдем мгновенный центр скоростей и обозначим его точкой Р (рис.1).

3). Определение скоростей точек и угловой скорости.

а). Определяем угловую скорость линейки АВ по формуле:

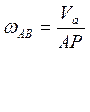
Из прямоугольного треугольника АВР находим АР.

      АР = см.

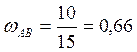  рад/с

б). Определяем скорость точки В по формуле:

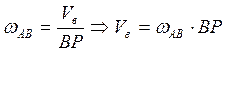
Из треугольника АВР определим ВР.

      ВР = АВ cos 30 = 26 см.     

V_в =  см/с 

в). Определяем скорость точки С по формуле:

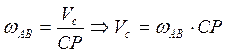
       Находим СР из треугольника АСР.

       СР²  = АР² + АС² – 2 АР АС cos 60 = 15² + 15² – 2 15 15 0,5 = 225

       СР = = 15 см.

   V_c = 0,66 15 = 9,9 см/с        

   Все найденные в ходе расчета скорости покажем на рисунке №1.

4). Определение ускорения точек и углового ускорения (рис. 2).

 а). Согласно теореме об ускорениях точек плоской фигуры, ускорение точки В определяется по следующей формуле:

     (1)

Определим центростремительное ускорение точки В относительно точки А.

  см/с²

Для того чтобы найти оставшиеся ускорения, проведем анализ уравнения (1).

Ускорение точки А по условию равно нулю.

Центростремительное ускорение точки В мы определили   .

Оно нам известно как по величине, так и по направлению. Вектор  направлен от В к А, следовательно мы можем смело показать данный вектор на рисунка №2.

Что касается ускорения  точки В и вращательного ускорения , то данные векторы не известны как по величине не по направлению, но известны только линии действия этих векторов. Предположим, что вектор  направлен вниз по вертикали вдоль направляющих ползуна, т.е. в туже сторону куда направлена скорость точки В. Вектор  направим перпендикулярно  к АВ и так же вниз.

Для того чтобы определить величину данных ускорений точек, спроецируем уравнение (1) на оси координат хВу.

1) Спроецируем уравнение (1) на ось х т.е. найдем  аналитическим способом.

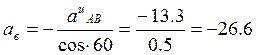    см/с

  Знак минус в ответе показывает, что истинное направление вектора  не соответствует принятому при расчете. Вследствие этого на рисунке №2 изменим направление вектора .   

2) Спроецируем уравнение (1) на ось у, тем самым найдем  аналитическим              способом.

  см/с²

Знак минус в ответе показывает, что истинное направление вектора  не соответствует принятому при расчете. Вследствие этого на рисунке № 2 изменим направление вектора .

б). Находим угловое ускорение линейки АВ по формуле:

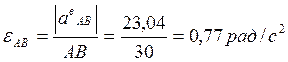
в). Определяем ускорение точки С по формуле:

   Находим вращательное и центростремительное ускорение точки С.

       см/с²

     см/с²

 Вектор  направлен от точки С, к точке А.

Вектор  перпендикулярен вектору  и направлен соответственно угловому ускорению .  

Для нахождения ускорения точки С, применим способ проекции на ось хВу.

а_Сх =  см/с²

а_Сх = -см/с²

 Определим полное ускорение точки С. 

а_С =  см/с²

Ответ:  V_в = 17,3 см/с           По полученным данным строим график

             V_c = 9.9  cм/с            скоростей (рис№1) и ускорений точек (рис№2).

  0,66 рад/с

  а_в = 26,6 см/с²

  а_с = 13,3 см/с²

  0,77 рад/с².