





















Функция индивидуального потребительского спроса и функции совокупного спроса и совокупных сбережений в неоклассической модели.
Спрос зависит от 4 субъектов сектор дом.х-в, предпринимательский сектор, гос-во и заграница.
Неоклассические функции потребления и сбережения.
В соответствии с неоклассиками действия индивида на всех рынках подчинены цели максимизации его благосостояния. Даже при экзогенно заданной цене факторов производства домашние хозяйства сами устанавливают величину своего дохода, определяя объёмы продаж принадлежащих им факторов производства. Распределение определённого таким образом сбережения тоже направлено на максимизацию многопериодной функции полезности.
Пусть
предпочтения индивида относительно 2-х благ — свободного времени (F) и получаемого за труд дохода (y)
отображаются ф-ей полезности U=![]() .
Задача индивида – так распределить какое-то календарное время, чтобы при
имеющихся возможностях получения дохода ф-я полезности достигла максимального
значения. Возможности получения дохода определяются ценами имеющихся у
дом.хоз-ва факторов производства: у=wN+rK. В текущем периоде объём капитала задан, и поэтому
повлиять на величину дохода индивид может только путём распределения
календарного времени на свободное и рабочее: T=F+N. Составляем функцию
Лагранжа: y=
.
Задача индивида – так распределить какое-то календарное время, чтобы при
имеющихся возможностях получения дохода ф-я полезности достигла максимального
значения. Возможности получения дохода определяются ценами имеющихся у
дом.хоз-ва факторов производства: у=wN+rK. В текущем периоде объём капитала задан, и поэтому
повлиять на величину дохода индивид может только путём распределения
календарного времени на свободное и рабочее: T=F+N. Составляем функцию
Лагранжа: y=![]() +
+![]() [w(T-F) + rK-y]. Дальше берутся 3 частные производные по у, F и
[w(T-F) + rK-y]. Дальше берутся 3 частные производные по у, F и ![]() . Из
производной по y, F следует,
что у= Fw, это подставляем в производную по
. Из
производной по y, F следует,
что у= Fw, это подставляем в производную по ![]() : wT–wF+rK–Fw=0 è 2wN=Tw-rK è N*=T/2 –rK/2w.
: wT–wF+rK–Fw=0 è 2wN=Tw-rK è N*=T/2 –rK/2w.
Вот столько времени посвятит хоз-во труду, что и определит его доход при заданных ценах.
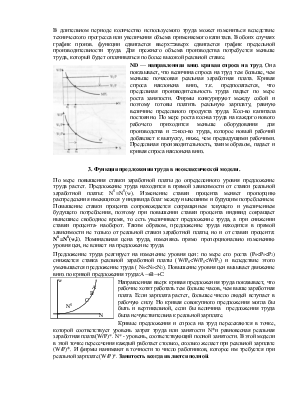
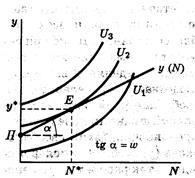 Графически рисуются кривые безразличия, как для антиблага , т.е. из
начала координат, с положительным наклоном, выпуклы к оси абсцисс (час труда
должен компенсироваться доп. доходом). Индивид стремится к всё большему доходу,
но мешается под ногами бюджетное ограничение: у=wN+rK, графически представленное прямой. Точка пересечения –
определяет величину дохода и объём предлагаемого труда.
Графически рисуются кривые безразличия, как для антиблага , т.е. из
начала координат, с положительным наклоном, выпуклы к оси абсцисс (час труда
должен компенсироваться доп. доходом). Индивид стремится к всё большему доходу,
но мешается под ногами бюджетное ограничение: у=wN+rK, графически представленное прямой. Точка пересечения –
определяет величину дохода и объём предлагаемого труда.
Распределение дохода между текущим С и S исходя из: (1) Степени его предпочтения текущего потребления будущему и (2) установившейся меры вознаграждения за отказ от текущего потребления (ссудной ставки %). В каждом периоде дом.х-во получает доход от труда и капитала, причём он (имущество) состоит из облигаций, приносящих % (i).
Тогда бюджетное ограничение в периоде t: Wt+Bt-1(1+i)=Ct+Bt, где Wt – трудовой доход в тек. периоде, Bt-1 – реальная ценность облигаций в предшеств. периоде, которая в тек. периоде доросла до Bt-1(1+i). Правая часть: часть бюджета потребляется (Сt), а другая – сберегается в виде облигаций (Bt). Разность Bt-1- Bt – это объём сбережений дом. хоз-ва в периоде t.
В целях упрощения анализа будет только 2 периода t=1, t=2. Бюджетные ур-я этих 2-х периодов: W1+B0(1+i)=C1+B1 и W2+B1(1+i)=C2+B2.
Из 1-го ур-я определяется значение B1 и подставляется во второе. В результате получилось: С1+С2/(1+i)=W1+W2/(1+i) +B0(1+i)-B2/(1+i).
Левая часть – дисконтированная сумма потребления за оба периода, правая – дисконтированная сумма имеющихся для потребления средств. Туда же идёт и изменение имущества (фонда облигаций). Обозначим правую часть Ур-я (1) буквой А и запишем эту штуку в виде уравнения двухпериодной бюджетной линии: C1=A-C2/(1+i).
Там идут кривые безразличия и бюджетное ограничение, они
пересекаются и – оптимум, показывающий, как распределяется потребление индивида
между 1-м и 2-м периодом. 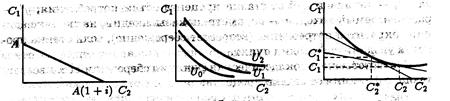 В случае повышения ставки % угол наклона бюджетной линии
уменьшится, и тогда тот же самый уровень благосостояния в двух смежных периодах
достигается
В случае повышения ставки % угол наклона бюджетной линии
уменьшится, и тогда тот же самый уровень благосостояния в двух смежных периодах
достигается
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.