Параметрический анализ и создание переходного патрубка турбовального газотурбинного двигателя, страница 7

          д) влияние режимных параметров. С качественной стороны рост режимных параметров оказывается такой же как и для конических диффузоров. На рис. 3.8 приведены результаты опытного исследования диффузоров при числах λ₁=0,3-1,0. Здесь во всех случаях при дозвуковых скоростях течение оставалось безотрывочным и всюду фиксировалось снижение потерь с ростом безразмерной скорости λ₁.

 

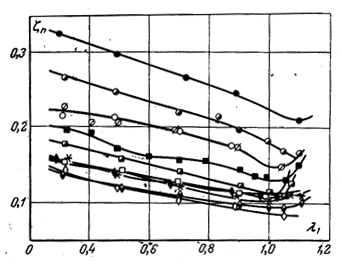
Рисунок 3.8 – Влияние сжимаемости на коэффициент ξ_п.

4.  Кольцевой диффузор с криволинейными образующими [4]

          Осерадиальные диффузоры, проточная часть и геометрические размеры которых приведены на рис 4.1, образованы двумя криволинейными соосными поверхностями вращения АВ и СD. Форма сечений этих диффузоров совпадает с формой сечений плоских криволинейных диффузоров.

         

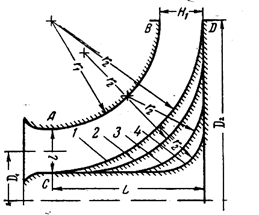
Рисунок 4.1 – Схема криволинейного кольцевого диффузора. Форма меридиональных сечений и основные обозначения

1 - ; 2 - ; 3 -  4 - .

В простейшем случае, когда образующие АВ и СD очерчены радиусами r₁ и r₂, безразмерными геометрическими параметрами будут:

n;    ; ;    ;    .

Экспериментальное исследование влияния геометрических параметров на работу кольцевых криволинейных диффузоров связано с большими трудностями. Они вызваны из-за того, что для характеристики диффузора необходимо задание шести безразмерных величин.

В результате при исследовании осерадиальных диффузоров ограничиваются геометрическими параметрами, влияние которых должно быть решающим.

Рассмотрим следующие безразмерные параметры диффузора: безразмерный диаметр на входе  , «радиальность» , «интенсивность» поворота  , безразмерный радиус   и степень расширения n.

Каждый из приведенных параметров имеет определенный физический смысл. Так,   характеризует входные условия и структуру и интенсивность вторичных течений,  определяет форму канала в меридиональном сечении диффузора,  показывает, сколь «резко» происходит поворот, и т.д.

а) Влияние радиусов r₁ r₂ и степени расширения n. Поскольку потери в кольцевых криволинейных диффузорах зависят в основном от распределения скоростей по обводам АВ СD, а последнее определяется формой меридионального сечения, выясним влияние радиусов r₁, r₂ и степени расширения n. Рассмотрим результаты опытного исследования диффузоров при различной форме меридиональных сечений. Эти сечения, приведены на рис. 4.1, очерчены неизменным радиусом r₁ и непрерывно уменьшающимся r₂.

Испытания указанных диффузоров, результаты которых представлены на рис. 4.2, свидетельствуют сто между радиусами r₁ и r₂ существует некоторое оптимальное соотношение, отклонение от которого при малых степенях расширения приводит к заметному увеличению потерь.

 

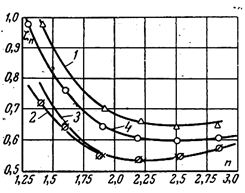Рисунок 4.2 – Зависимость потерь в осерадиальных диффузорах

от степени расширения n при различных отношениях радиусов .

1 - ; 2 - ; 3 -  4 - .

Для большей наглядности на рис. 4.3 изображена зависимость ξ_п=f(), полученая в зоне оптимальныхвеличин n (n_опт=2.2-2.3).

Из приведенной кривой следует, что с увеличением  вначале происходит некоторое снижение потерь. При =0,7-1,1 потери достигают минимального значения и затем для  довольно резко возрастают. Такой характер изменения потерь связан с формой канала в меридиональном сечении диффузора или, точнее, с характером изменения скорости вдоль выпуклого АВ и СD рис. 4.1 обводов, образующих канал.

 

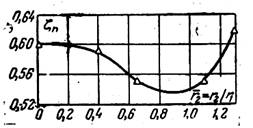Рисунок 4.3 – Изменение потерь в зависимости от  в зоне

оптимальных степеней расширения.

б) влияние относительной длинны («интенсивности» поворота). Следующим весьма важным геометрическим параметрам осерадиального диффузора является безразмерная длинна .

Данные, приведенные на рис. 4.4, свидетельствуют, что с увеличением безразмерного расстояния  происходит непрерывное уменьшение коэффициента полных потерь и возрастает оптимальная степень расширения. Геометрически с ростом  осерадиальные диффузоры приближаются к осевым кольцевым диффузорам. При этом доля потерь, связанная с поворотом потока, непрерывно должна уменьшатся.

 

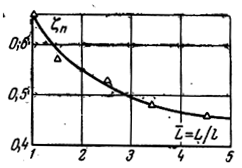Рисунок 4.4 – Зависимость коэффициента полных потерь ξ_п

от параметров