Параметрический анализ и создание переходного патрубка турбовального газотурбинного двигателя, страница 3

Опытные данные, приведенные на рис. 1.3 показывают, что при больших числах Re₁ изменение угла α до некоторого критического значения α_кр почти не меняет коэффициента восстановления энергии, а при α > α_кр происходит резкое его снижение, вызванное отрывом потока.

 

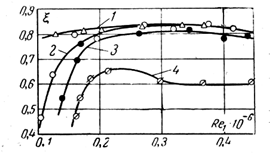Рисунок 1.3 – Зависимость коэффициента ξ от Re₁  и угла α. (n=4; λ=0.8).

1 – α = 7⁰; 2 – α  =10⁰; 3 - α =15⁰; 4 – α =20⁰.

Величина критического угла зависит от степени расширения, числа Re₁ и безразмерной входной скоростью λ₁. Для малых скоростей и больших чисел Re₁ значение α_кр определяется кривой рис. 1.4, и показывает, что с увеличением степени расширения происходит снижение критического значения угла α_кр.

 

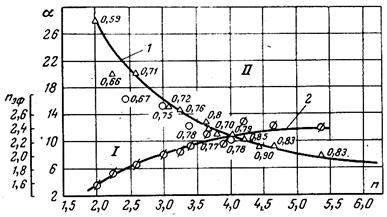Рисунок 1.4 – Линия предельных параметров безотрывных

плоских и конических диффузоров

1 – зависимость α =f(n); о – опыты МЭИ; ∆ - данные Кляйна; 2 – зависимость n_эф =f(n)

          На рис. 1.4 построена предельная кривая 1, разделяющая всю область α (n) на две части: безотрывных диффузоров (область Ι) и отрывных (область ΙΙ); цифры у экспериментальных точек соответствуют значениям коэффициента восстановления энергии.

          Приведенные результаты опытов устанавливают тесную взаимосвязь между степенью расширения n и максимальным углом раскрытия диффузора α_кр. Область предельных геометрических параметров, отделяющих безотрывное течение от отрывного, в плоских и конических диффузорах весьма значительна.

          Влияние режимных параметров на потери в диффузоре является не однозначны и зависит от геометрических характеристик диффузоров.

          Опытные данные, полученные при одновременном изменении чисел М и Re, существенно затрудняют анализ влияния каждого параметра в отдельности.

         

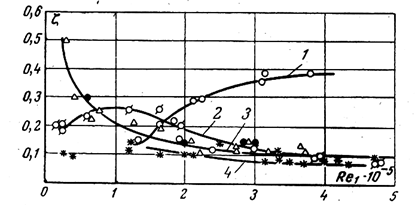
Рисунок 1.5 – Изменение коэффициентов потерь ξ_п в зависимости от числа Re₁ (n=4; М₁=0,5)

1 – α =20⁰; 2 – α =15⁰; 3 - α =10⁰; 4 – α =4⁰

          Была исследована зависимость потерь от числа Re₁ для конических с различными углами раскрытия.

          Результаты испытаний диффузоров с независимым моделированием по числам Маха и Рейнольдса отражены на рис. 1.5 [3].

          Для каждой рассматриваемой кривой число М₁ сохранялось неизменным, т.е. данные отражали только влияние числа Re₁. Движение газа в диффузоре с углом α =20⁰ увеличение числа Re₁ вызывало рост потерь, величина которых асимптотически стремилась к некоторому постоянному значению В то же время в диффузорах с углами  α =15 и 10⁰ потери интенсивно снижались и приближались  к постоянным значениям при Re₁>5*10⁵. Нанесенные на рис. 1.5 потери для диффузоров с углом раскрытия α = 4⁰ и n = 3,5 практически оказалось не зависящим от числа Рейнольдса. Это обстоятельство связано с тем, что при малых углах α течение в диффузоре во всем диапазоне чисел Re₁ является без отрывочным независимо от режима течения в пограничном слое.

2.  Характеристики плоского криволинейного диффузора [4]

          Рассматривая плоский криволинейный диффузор, следует отметить, что в сравнении с прямолинейными диффузорами минимальное число геометрических параметров, определяющих форму проточной части в меридиональном сечении, заметно возрастает.

          Так в простейшем случае при искривлении канала добавляется еще одна переменная Δβ, характеризующий угол этого искривления рис. 2.1.

Рассматривая плоский криволинейный диффузор рис. 2.2, следует отметить, что здесь минимальное число геометрических параметров, определяющих форму проточной части в меридиональном сечении, становится еще больше.

 

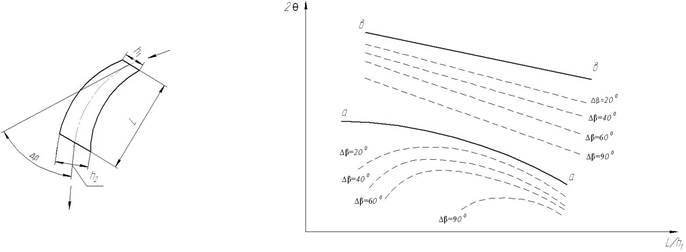Рисунок 2.1 – Схема простейшего криволинейного диффузора

и безотрывного, и отрывного течения 

 

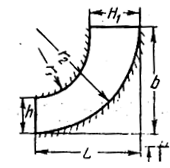Рисунок 2.2 -  Схема плоского криволинейного диффузора

Так необходимо задать его длину L, размер b, радиусы r₁ и r₂ и высоты h₁ и h₂.

          Сохранив и здесь в качестве определяющего размера h₁, получим следующие безразмерные величины:

;  ;  ;  ;   .

          Учитывая, однако что течение в криволинейном канале существенно зависит от радиуса , в некоторых случаях имеет смысл принимать за определяющий размер не h, а радиус . Но как и в первом, так и во втором случаях при оценке подобия криволинейных диффузоров необходимо обеспечить равенство по крайней мере трех безразмерных величин: n, , и . Первый из этих параметров характеризует степень расширения диффузоров, второй форму канала, а третий указывает на его относительную кривизну.