Данное выражение показывает, что подведенная к телу механическая работа расходуется на повышение давления рабочего тела (совершение политропической работы сжатия), изменение кинетической энергии и преодоление сил трения. Чаще это уравнение называют обобщенным уравнением Бернулли, т.к. оно выводилось для изолированных процессов.
ЛЕКЦИЯ №4
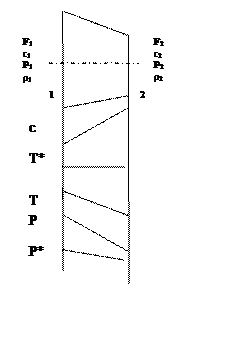
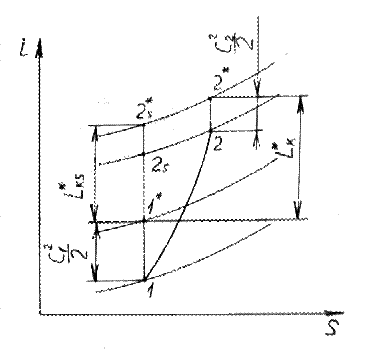
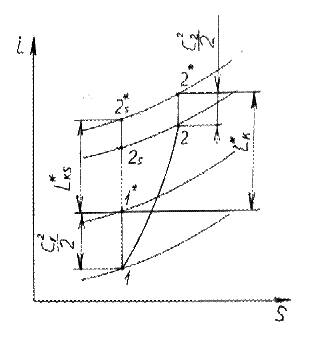
Изображение процессов проточной части двигателя в i–S диаграмме (тепловой диаграмме).
Энергетически изолированные процессы (идущие без подвода/отвода механической энергии из вне).
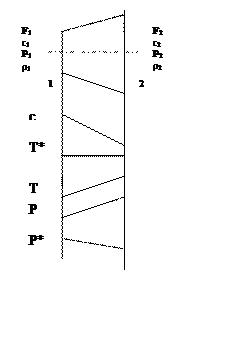 В курсе теории и расчета лопаточных
машин принимают, что энергетически изолированные процессы протекают во входных
устройствах, соплах, направляющих и сопловых аппаратах.
В курсе теории и расчета лопаточных
машин принимают, что энергетически изолированные процессы протекают во входных
устройствах, соплах, направляющих и сопловых аппаратах.
Рассмотрим процесс повышения давления в диффузорном канале.
Запишем уравнение
расхода. При этом условимся, что ![]()
![]()
![]() .
.
Для энергоизолированной (![]() ) системы уравнение теплосодержания примет
следующий вид
) системы уравнение теплосодержания примет
следующий вид
![]()
![]() ,
,
![]() ,
,
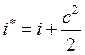 ,
,
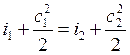 ,
,
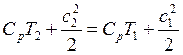 ,
,
![]() .
.
Запишем уравнение Бернулли
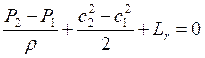 ,
,
примем ![]() , тогда при
, тогда при ![]() давление
будет расти,
давление
будет расти, ![]() .
.
Рассмотрим 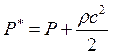 – запас энергии, способной совершать механическую
работу или давление заторможенного потока.
– запас энергии, способной совершать механическую
работу или давление заторможенного потока.
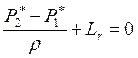 ,
,
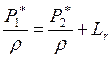 .
.
Рассмотрим теперь тепловую диаграмму. И энтропия, и энтальпия – функции состояния вещества
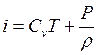 ,
, 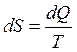 ,
, 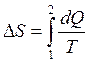 .
.
Все реальные процессы сопровождаются ростом энтропии.
Изоэнтропическими
процессами называют такие процессы, в ходе которых энтропия остается неизменной,
![]() .
.
Сам по себе процесс торможения – условный, т.е. он идет без потерь.
Рассмотрим реальный процесс, протекающий в диффузоре.

![]()
Для энергоизолированного процесса энтальпии на входе и на выходе одинаковы.
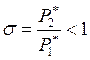 –
коэффициент, характеризующий потери полного давления, затраченные на преодоление
сил трения.
–
коэффициент, характеризующий потери полного давления, затраченные на преодоление
сил трения.
Рассмотрим процесс расширения в конфузорных каналах.
 Запишем уравнение расхода
Запишем уравнение расхода
![]() ,
,
![]() ,
,
Для энергоизолированной (![]() ) системы уравнение теплосодержания примет
следующий вид
) системы уравнение теплосодержания примет
следующий вид
![]()
![]() ,
,
![]() ,
,
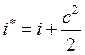 ,
,
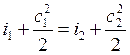 ,
,
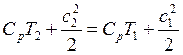 ,
,
![]() .
.
Запишем уравнение Бернулли
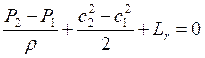 ,
,
примем ![]() , тогда при
, тогда при ![]() давление
будет падать,
давление
будет падать, ![]() .
.
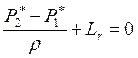 ,
,
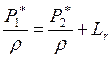 .
.
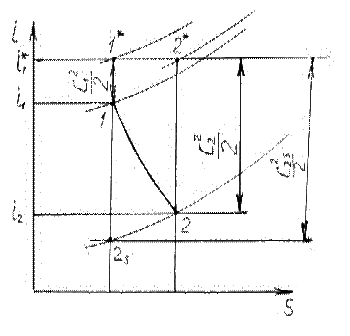
![]() –
скорость изоэнтропического (идеального) потока.
–
скорость изоэнтропического (идеального) потока.
Часто потери в сопловом
аппарате определяют коэффициентом скорости – 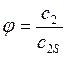 .
.
Процессы с подводом и отводом энергии.
В компрессорах ГТД к рабочему телу подводится энергия в виде механической работы, т.е.
![]() , тогда уравнение теплосодержания примет
следующий вид
, тогда уравнение теплосодержания примет
следующий вид ![]() . Для определения полного
давления воспользуемся уравнением Бернулли
. Для определения полного
давления воспользуемся уравнением Бернулли 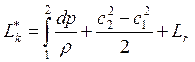 .
Пренебрегая изменением плотности ρ, получим
.
Пренебрегая изменением плотности ρ, получим 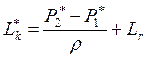 .
Работа потерь
.
Работа потерь ![]() пренебрежимо мала по сравнению с
механической работой компрессора
пренебрежимо мала по сравнению с
механической работой компрессора ![]() , следовательно
, следовательно ![]() .
.
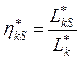 –
изоэнтропический КПД компрессора по заторможенным параметрам.
–
изоэнтропический КПД компрессора по заторможенным параметрам.
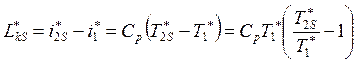 ,
,
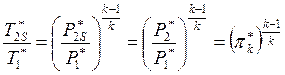 ,
,
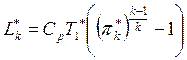 .
.
В турбине ГТД, в отличие от компрессора, работа совершается самим газом, т.е.
![]() .
.
Запишем основные уравнения для данного процесса.
![]() ,
,
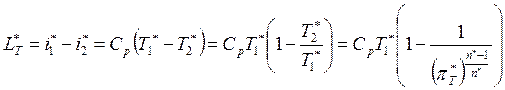 ,
,
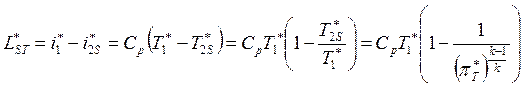 ,
,
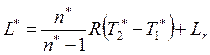 ,
,
![]() ,
,
тогда 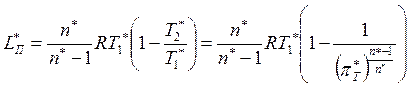 .
.
В данных выражениях ![]() – работа турбины по заторможенным
параметрам,
– работа турбины по заторможенным
параметрам, ![]() – изоэнтропическая работа турбины по
заторможенным параметрам,
– изоэнтропическая работа турбины по
заторможенным параметрам, ![]() – политропическая
работа турбины по заторможенным параметрам.
– политропическая
работа турбины по заторможенным параметрам.
Способы выражения потерь в элементах лопаточных машин.
Процесс сжатия в направляющем аппарате компрессорной ступени характеризуется коэффициентом восстановления полного давления.
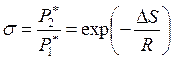 .
.
Процесс расширения в
сопловом аппарате турбины зависит от коэффициента скорости 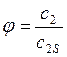 .
.

Процесс сжатия в компрессоре.
Изоэнтропический КПД компрессора по полным параметрам
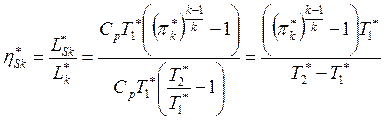 .
.
Изоэнтропический КПД по статическим параметрам
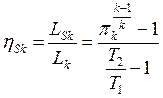 .
.
Политропический КПД по заторможенным параметрам
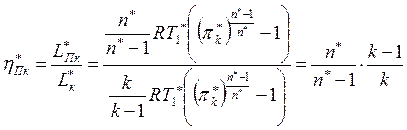 .
.
Политропический КПД компрессора учитывает только гидравлические потери проточной части; изоэнтропический же КПД, кроме того, учитывает наличие теплового сопротивления в процессе сжатия.
 Процесс расширения
в турбине.
Процесс расширения
в турбине.
Изоэнтропический КПД турбины.
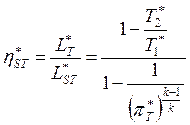 .
.
Политропический КПД турбины
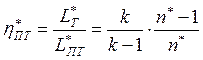 .
.
Мощностной (эффективный) КПД турбины
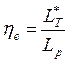 ,
где
,
где ![]() – располагаемая работа (от
– располагаемая работа (от ![]() до
до ![]() ).
).
По сравнению с изоэнтропическим КПД по заторможенным параметрам эффективный КПД учитывает потери, связанные с выходной скоростью.
ЛЕКЦИЯ №6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.