Определение коэффициента внутреннего трения жидкости методом падающего шарика (метод Стокса): Методические указания к лабораторной работе № 14, страница 2

Молекулы газов движутся по прямолинейным траекториям, направление которых изменяется при столкновениях молекул. Тепловое движение молекул в жидкости есть чередование колебаний около некоторых положений равновесия (в периоды „оседлой жизни”, подобной тепловому движению частиц твердого тела) с перескоками из одного положения равновесия в другое, подобными тепловому движению газовых молекул („кочевая жизнь”).

Если жидкость в целом находится в покое, то все направления этих перескоков равновероятны; если же жидкость течет, то преобладают те направления перескоков, которые образуют небольшие углы с направлением течения жидкости. В этом и заключается наложение упорядоченного движения жидкости на хаотическое движение молекул.

Так как молекулы жидкости большую часть времени находятся около положений равновесия (т.е. оседлая жизнь преобладает над кочевой), то движущаяся масса жидкости увлекает соседние слои в основном за счет сил сцепления.

С ростом температуры оседлая жизнь молекул сокращается, т.е. перескоки из одного положения равновесия в другое становятся чаще.

Молекула жидкости может проникать из одного слоя в другой лишь при наличии в последнем ,,дырки’’, т.е. полости, достаточной для перескакивания туда молекулы. При значительном повышении давления число таких дырок существенно уменьшается. Это объясняет увеличение вязкости жидкости при высоких давлениях.

2. Движение тела в вязкой среде

Рассмотрим равномерное движение тела в вязкой среде, т.е. внутри жидкости. При движении пластины в жидкости тонкий ее слой будет прилипать к поверхности пластины и двигаться с ней, как одно целое, увлекая за собой из-за трения последующие слои. По мере удаления от поверхности тела скорость жидкости уменьшается и на некотором расстоянии от поверхности тела жидкость остается практически невозмущенной движением тела. Таким образом движущиеся тела оказываются окруженными слоем жидкости, в котором имеется градиент скорости. Этот слой жидкости называют пограничным. В нем действуют силы трения, которые в конечном итоге оказываются приложенными к телу и приводят к возникновению лобового сопротивления.

Объяснение лобового сопротивления внутренним трением справедливо только при небольших скоростях движения. При увеличении скорости начинает играть роль разность давлений перед движущимся телом и сзади него, что приводит к возникновению так называемого сопротивления давления. Соотношение между сопротивлением трения и сопротивлением давления определяется значением безразмерной величины, называемой числом Рейнольдса и обозначаемого :

,                                       (4)

где  - скорость движения тела, а - некоторый характерный размер тела, например для шара его радиус.

При малых значениях числа Рейнольдса (<<1), когда основную роль играет сопротивление трения, сила сопротивления неограниченной вязкой среды движению шарика радиуса  (диаметра ) может быть подсчитана по формуле Стокса:

                           (5)

3. Определение коэффициента вязкости жидкости методом падающего шарика

Формула Стокса позволяет определить коэффициент вязкости жидкости, наблюдая за падением в ней небольшого шарика.

На шарик после начала движения действуют три силы: сила тяжести , направленная вертикально вниз, выталкивающая архимедова сила  и сила сопротивления среды  направленные вертикально вверх. Первые две силы постоянны по величине, а сила сопротивления пропорциональна величине скорости движения. Поэтому скорость падения шарика будет сначала увеличиваться, но только до тех пор, пока она не достигнет такого значения скорости , при котором выполнится следующее условие:

.                                     (6)

Начиная с этого момента , шарик будет двигаться равномерно со скоростью . Решение дифференциального уравнения движения показывает, что участок, в течение которого происходит нарастание скорости, чрезвычайно мал. Поэтому с достаточной точностью можно считать, что шарик движется равномерно и отсчет времени начинать от начала движения шарика.

Формулу (6) можно применить для движения как однородного, так и неоднородного шарика.

1.   Однородный шарик. Для однородного (т.е. не имеет пустот) шарика диаметром  и плотностью  можно записать, что:

 , а    ,                 (7)

где - плотность жидкости, а - ускорение свободного падения. Подставляя (5) и (7) в (6) получаем для коэффициента вязкости формулу:

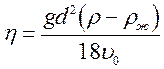 .                            (8)

Если замерить время падения  шарика на участке пути , то формула (8) приобретет вид:

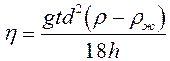 .                         (9)

2. Неоднородный шарик. Если шарик неоднородный по объему, (например пластмассовый шарик с наличием в нем металлического стержня) или плотность вещества шарика неизвестна, то зная массу шарика формулу (9) можно привести к виду:

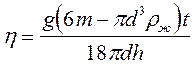.                       (10)

4. Описание лабораторной установки