Определение коэффициента внутреннего трения жидкости методом падающего шарика (метод Стокса): Методические указания к лабораторной работе № 14

1. Внутреннее трение в газах и жидкостях, как одно из

     явлений переноса

Хаотическое движение молекул лежит в основе процессов, объединяемых общим названием „явления переноса”. Явлениями переноса называют процессы, при которых благодаря беспорядочному тепловому движению молекул происходит перенос какой-нибудь макроскопической величины из одного места газа или жидкости в другое.

Рассмотрим явление переноса, характеризующее процесс внутреннего (вязкого) трения в газах и жидкостях.

Для этого представим, что внутри сосуда с газом, над его плоским дном (совпадающим с горизонтальной плоскостью YOZ координатной системы) движется в направлении оси Z параллельно дну плоская пластина, линейные размеры которой значительно превосходят ее расстояние до дна сосуда и при этом скорость  движения пластины во много раз меньше средней скорости хаотического движения молекул. Опыт показывает, что для равномерного движения пластины необходимо действовать на нее с вполне определенной силой , которая должна уравновесить препятствующую этому движению силу внутреннего трения. Каково происхождение этой силы?

Необходимо учесть, что молекулы газа, непосредственно соприкасающиеся с пластиной, как бы прилипают к ней. Иными словами на беспорядочное тепловое движение этих молекул накладывается упорядоченное движение пластины с „прилипшими” молекулами.

При удалении от пластины по направлению ко дну сосуда скорость упорядоченного движения слоев газа уменьшается и для слоя, непосредственно соприкасающегося с дном сосуда, обращается в нуль. Изменение вектора скорости упорядоченного движения при переходе от одного слоя газа к другому отображено на эпюре скоростей (стрелки, приведенные на рис. 1).

            Быстрота изменения скорости  в направлении оси Х может быть охарактеризована величиной, которая называется градиентом скорости.

Для того чтобы дать молекулярно-кинетическое истолкование сил внутреннего трения, рассмотрим два смежных слоя газа, т.е. таких, координаты которых вдоль оси Х отличаются на . Пусть площадь каждого слоя S, скорость упорядоченного движения одного слоя , другого  (рис. 2).

Молекулы одного из слоев не отличаются энергией от молекул другого слоя, поскольку температура обоих слоев одинакова. Но среднее значение составляющей скорости по направлению упорядоченного движения различно. В нашем примере у молекул верхнего слоя эта скорость больше, чем у молекул нижнего слоя.

Поскольку все направления хаотического теплового движения равновероятны, то в результате теплового движения некоторые молекулы будут перелетать из верхнего слоя в нижний, другие в обратном направлении. При этом молекулы будут переносить с собой некоторый импульс, направленный в сторону упорядоченного движения слоев.

Перелетая из верхнего слоя в нижний, молекулы обогащают его импульсом, т.е. ускоряют упорядоченное движение нижнего слоя. Перелетая из нижнего слоя в верхний, молекулы затормаживают его движение, т.е. отбирают у верхнего слоя некоторую часть импульса. Совокупность этих процессов приводит к тому, что из одного слоя в другой (в данном случае из верхнего слоя в нижний) переносится импульс , связанный с упорядоченным движением слоя газа.

В установившемся потоке, т.е. при таком состоянии текущего газа (жидкости), при котором скорости слоев не изменяются со временем, величина переносимого импульса определяется как:

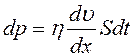,                                     (1)

где - динамический коэффициент вязкости газа. Единицей динамической вязкости в системе СИ является паскаль-секунда (Па^.с).

Преобразуем формулу (1), вводя в рассмотрение действующую между слоями газа и касательную к их поверхностям силу внутреннего трения. Используя второй закон Ньютона получаем:

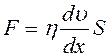,                                        (2)

Наряду с динамической вязкостью внутреннее трение в газах и жидкостях характеризуют кинематической вязкостью:

,                                               (3)

где  - плотность газа или жидкости .

Необходимо отметить, что механизм возникновения внутреннего трения в жидкостях отличается от рассмотренного выше механизма возникновения внутреннего трения в газах. Это связано с различием характера теплового движения в газах и жидкостях.