Расчёт антенны типа “волновой канал”, страница 3

Из таблицы найдём максимальное значение отношения . Максимальным оно будет при , а соответствующее ему значение сопротивления равно .

С помощью программы MathCAD построим график зависимости  от сопротивления  при .

         Получившийся график представлен на рисунке 1.

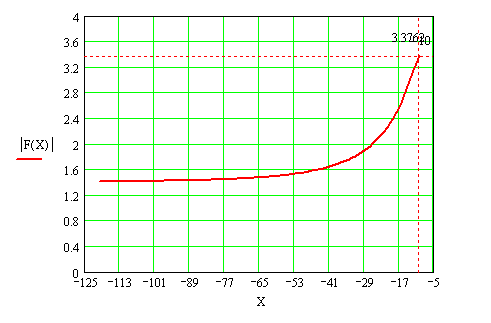
Рисунок 1 – Зависимость напряженности поля от собственного сопротивления активного вибратора при .

По результатам расчетов делаем вывод: максимальное значение отношение  достигается при значении собственного сопротивления , расстоянии между директорами , . Таким образом, дальнейшие расчёты будут вестись при найденных значениях ,  и .

Определим токи в вибраторах без учета рефлектора по формулам (2), (4), (5), (7), (8), (9):

2. Определение оптимального сопротивления рефлектора

         Для определения оптимального сопротивления рефлектора воспользуемся значениями токов и сопротивлений, вычисленных ранее. Так же как и в предыдущем пункте построим графики изменения напряжённости поля от изменения собственного сопротивления рефлектора.

         Для антенны с рефлектором система уравнений имеет вид [1]:

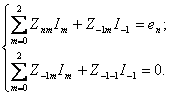(10)

Рекуррентные соотношения для нахождения токов в антенне имеют вид [1]:

;

;

,

где .

Токи в антенне с рефлектором находятся следующим образом [1]:

;                    (11)

;                                                               (12)