Вариант ВОриентир стоит непосредственно у уреза воды и вертикальный угол измеряется между береговой линией и вершиной ориентира.
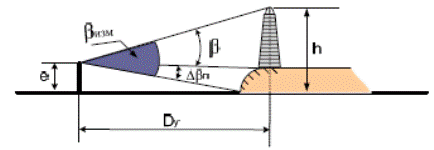
Порядок действий такой же, как в первых семи пунктах варианта А, только счислимое расстояние от судна до ориентира Dcв этом варианте равно расстоянию от судна до уреза воды Dп, снимаемому с карты. Dу 1 получают по табл. 2.7 МТ-2000.
Уточнение решения.
8. За уточненное расстояние до препятствия (уреза воды) принимают
Dп2= Dу1-l
По Dп 2 и e из табл. 3.20 МТ-2000 выбирают уточненную поправку за наклонение зрительного луча ∆βп2. Если ∆βп2= ∆βп1, то на этом расчет заканчивают, принимая за окончательное расстояние DУ =Dy1. Если ∆βп2 не равно ∆βп1 продолжают решение.
9. Рассчитывают уточненный угол β2 над истинным горизонтом.
β2 = βизм +(–∆βп2)
10. По h-eи β2 из табл. 2.7 МТ-2000 выбирают уточненное расстояние Dy. Приближенно Dy можно рассчитать по формуле
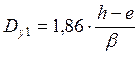
Схема решения приведена в примере 3.
Пример 3. Измерен вертикальный угол ос= 0°35,8′, i+s= + 0,5′ от уреза воды до фонаря маяка, стоящего непосредственно на самой оконечности берега. Высота ориентира h= 120 м., высота глаза наблюдателя е= 14 м. Расстояние до маяка с карты Dс= 5,3 мили.
е= 14м→ Де = 7,8 мили. т.к. Dс<Де , то для получения угла над истинным горизонтом надо ввести поправку ∆βп.
h = 120 м Dп 1=Dс= 5,3 мили ос = 0°35,8′
– +
е = 14 м i+s = + 0,5′
h-e = 106 м βизм = 0°36,3′
+
∆βп1 = – 7,1′ табл.3.20 МТ-2000
β1 = 0°29,2′
Dy1 =6,3 милитабл. 2.7 МТ-2000
Уточнение решения:
Dп2= Dy1= 6,3 мили βизм = 0°36,3′
+
∆βп = – 6,8′ табл. 3.20 МТ-2000
β 2 = 0°29,5′
Dy2 = 6,2 мили табл. 2.7 МТ-2000
Приближенное решение по формуле
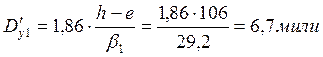
В задачах 201-300 измерен вертикальный угол ориентира между береговой линией и вершиной ориентира, стоящего непосредственно у уреза воды. Определить расстояние до ориентира Dy.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.