Второй случай.Расстояние Dcнебольшое, меньше дальности видимого горизонта. (Dc<Дe)
Возможны три варианта решения.
В вариантах А и В вертикальный угол измеряется от береговой линии
(черты) до вершины ориентира. Необходимо всегда иметь в виду, что в приливных морях положение уреза воды может меняться. При этом будет изменяться не только удаление ориентира от уреза воды, но и высота ориентира, используемая при определении расстояния. Поэтому в таких случаях необходимо вводить поправку на высоту ориентира за счет прилива.
Но даже с учетом этой поправки полученное расстояние может быть не совсем точным за счет погрешностей в высоте прилива и в снятом с карты удалении ориентира от береговой черты.
Вариант А.Ориентир удален от береговой черты и вертикальный угол измеряется между береговой линией (урезом воды) и вершиной ориентира.
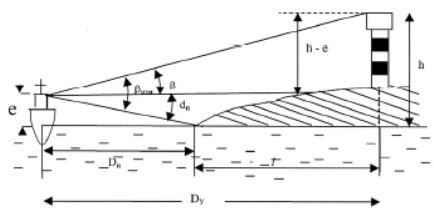
1. Измеряют вертикальный угол βизм от уреза воды до вершины
βизм=ОС+(i+s), угл. мин.
2. С карты снимают расстояние lот уреза воды до ориентира, мили.
3. Рассчитывают приближенное расстояние от судна до уреза воды D n1,мили.
Dп(расстояние до препятствия- так оно названо в МТ-2000)
Dп 1= Dc- l, где Dc- расстояние от счислимого места судна до ориентира. ( Dп 1 можно снять и прямо с карты).
4. По высоте глаза eи Dп1из табл. 3.20 МТ-2000 выбирают поправку за наклонение зрительного луча ∆βп 1, угл. мин.
5. Рассчитывают углы β над истинным горизонтом:
β 1= βизм+(-∆βп1).
6. Рассчитывают разность высот ориентира и глаза наблюдателя h-e,
метры.
7. По h-eи β 1 из табл. 2.7 МТ-2000 выбирают приближенное расстояние D′ y.
8. Вычисляют поправку по формуле
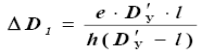
9. Рассчитывают искомое расстояние в первом приближении
Dу 1 = D'у + ∆D1
Для более точного нахождения расстояния решение продолжают.
10. Уточняют расстояние до береговой черты
Dп2=Dy1- l
11. По Dп2и е из табл. 3.20 МТ-2000 выбирают уточненную поправку за наклонение зрительного луча ∆βп2.
12. Рассчитывают уточненный угол над истинным горизонтом:
β2=βизм+(- ∆βп2).
13. По h-eи β2 из табл. 2.7 МТ-2000 выбирают расстояние D′y2.
14. Рассчитывают уточненную поправку
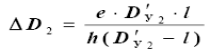
15. Рассчитывают более точное искомое расстояние
Dy2=D′y2+∆D2
Вместо действий 7-9 можно воспользоваться приближенной формулой
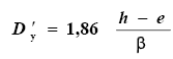 (2)
(2)
После чего уточнить расстояние до береговой черты
Dп2=Dy1- l
и выбрать по нему ∆βп2, рассчитать угол
β2= βизм+(–∆βп2).
По h-eи β2 по формуле (2) найти Dy.
Схема решения приведена в примере 2.
Пример 2Измерен вертикальный угол ос= 121,8', i+s=–1,1'между береговой линией и вершиной приметного навигационного ориентира, отстоящего от уреза воды на удалении l= 2 мили. Высота ориентира h= 317 м., высота глаза наблюдателя е= 15м. Расстояние до ориентира с карты Dс= 4,5 мили.
е= 15м→ Де=8,1 мили Dc = 4,5 мили
–
l= 2,0 мили
Dп1= 2,5 мили т.к. Dп1<Де, то для получения угла над истинным горизонтом надо ввести поправку за наклонение зрительного луча ∆βп.
h = 317 м ос = 1˚21,8′
- +
е = 15 м i+s = -1,1′
h-e= 302 м βизм =1˚20,7′
+
∆βп 1= -12,2′ табл. 3.20 МТ-2000
β1 =1˚08,5′→ D′y1= 7,9 мили табл. 2.7 МТ-2000
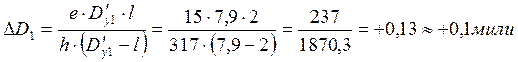
D′y1 = 7,9 мили Dy1 = 8,0 мили βизм = 1˚ 20,7′
+ – +
∆ D= +0,1 мили l=2,0 мили ∆βп 2= -7,2′ табл. 30 МТ-2000
Dy1 = 8,0 мили Dп 2 =6,0 мили β2 = 1° 13,5′→ D′y2 = 7,3мили
+ (табл. 2.7)
∆ D2 =+0,1мили
Dy2 = 7,4 мили
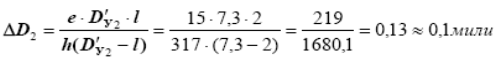
Приближенное решение
![]()
Dy1 =8,2 мили βизм = 1°20,7′
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.