О возможности использования математической модели для целей повышения точности инерциальных систем навигации, страница 2

Также решения уравнения (10) для каждого слагаемого правой части, пронумерованные числами от 1 до 5 (т.е. ,и т.д.) при условии, что начальные значения (0) и (0) имеют нулевые значения,(что для математической модели, безусловно, обеспечивается)получены в следующем ви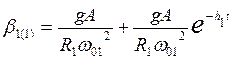де:

(+)(где =);

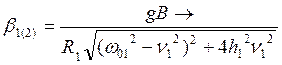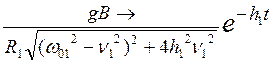
сos()+

(cos cos +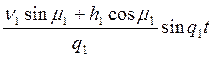); (где ).

;

;

;

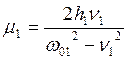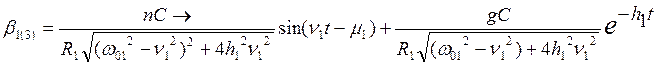
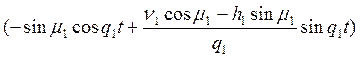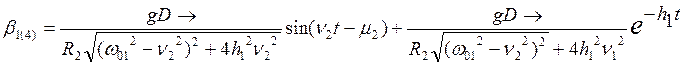
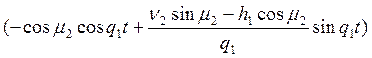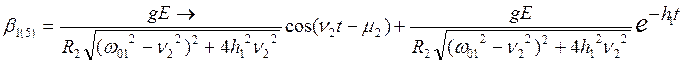
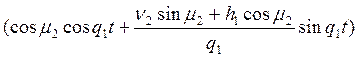В компактном виде полное решение для  имеет вид: =                                                                     (11)

Аналогичным образом пронумерованные слагаемые решения по переменной  получены в следующем виде:

;

;

;

;

.

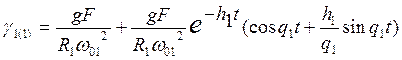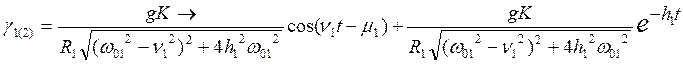
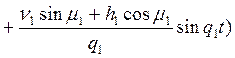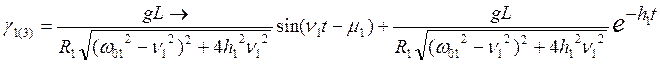
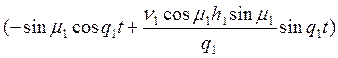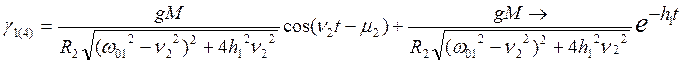
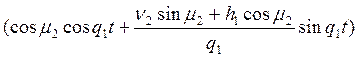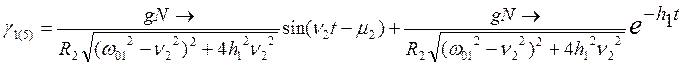
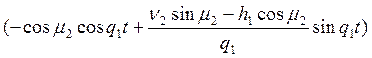В компактном виде полное решение для переменной  имеет вид:

=.                                                                       (12)

В полученных решениях для  и для  выполним следующие преобразования:

1)  Коэффициентом пропорциональности R₁ и R₂ придадим следующие значения (подчеркнем, что на нижеследующие значения не налагаются никакие ограничения)

,

.

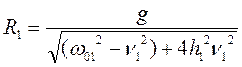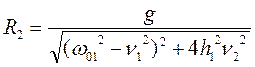2)  Путем подбора необходимого значения коэффициента затухания h₁ обеспечиваем практически полное устранение слагаемых, характеризующих сопутствующие колебания, причем за требуемый (необходимый) интервал времени. В результате первое слагаемое, составляющее полное решение , примет значение:

=А,

второе слагаемое

или

Необходимо сделать сдвиг по фазе  (тогда будут обеспечены требуемые значения, а именно: cos  sin .)

В полученных решениях для всех слагаемых  (см. выражение (12)), а также для всех слагаемых g₁ (см.- выражение (13)) выполним следующие преобразования: 

1) Коэффициентам пропорциональности R₁ и R₂ придадим следующие значения (подчеркнем, что на нижеследующие значения не налагаются никакие ограничения)

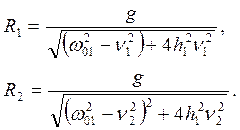
2) Путем подбора необходимого значения коэффициента затухания h₁ обеспечиваем практически полное устранение слагаемых, характеризующих сопутствующие колебания, причем за требуемый (необходимый) интервал времени. В результате первое слагаемое b₍₁₎, входящее в полное решение b, примет следующий вид

Второе слагаемое приобретет форму

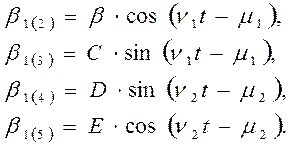
Третье

Четвертое

Пятое

Выражения b₍₂₎ - b₍₅₎ можно выразить в следующей тождественной форме:

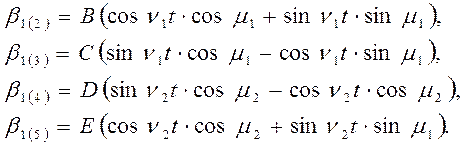
Придаем сдвигам по фазе m₁  и m₂ следующие значения

m₁=p, m₂=p (т.е , а )

Примечание: сдвиг по фазе, имеющие значения m₁=П, m₂=П ни при каких значениях величин, (физически всегда отличны от нуля и бесконечности),входящих в формулы сдвига по фазе невозможно обеспечит значения

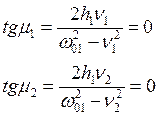
получены быть не могут. По этой причине в микропроцессорах в качестве математической модели должны закладываться не дифференциальные уравнения а их решения.

Вернемся к основному тексту.

После всех преобразований окончательное значение b₁ принимает следующий вид

                                         (14)

Соответственно, после аналогичных преобразований, окончательные значения g₁ будет определяться следующим выражением

   (15)

При выполнении в сумматоре сложения значений b (формула (6)) и b₁ (формула (14)), представленных в цифровой форме, получим

(16)

                                                                     (16)

Аналогично в другом сумматоре, при выполнении операций сложения значений g (формула (8)) и g₁ (формула (15)), также представленных в цифровой форме, будет иметь

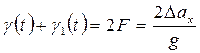(17)

                                                        (17)

Таким образом, в результате проделанных операций в суммарном сигнале обоих каналов на выходе сумматоров S₁ и S₂ произошло полное исключение составляющих угловых скоростей дрейфа гироскопических чувствительных элементов d_x, d_y, d_z .Изложенное иллюстрируется функциональной схемой на рис. 1 (для выходного сигнала акселерометра A_N (координата b)).

Аналогичная функциональная схема может быть представлена для выходного сигнала акселерометра А_Е (координата g). Отметим, что сигналом W_NK (для восточного канала - W_EK ) отмечены ускорения коррекции за счет действия кориолисовых и переносных ускорений..

2.4. Основные выводы

 В качестве заключения выполненного исследования сформулируем основные (ключевые) положения.

1. Ошибка по углу b движения механического аналога стабилизированной платформы отображается дифференциальным уравнением 3^a и определяется решением 4^a.

2. Ошибка по углу b₁ вычисляется в микропроцессоре №1, в который заложена математическая модель стабилизированной платформы в виде дифференциального уравнения (10), в котором внешнее возмущающее воздействие сформировано на основе выходного сигнала северного акселерометра. Решение дифференциального уравнения указанной математической модели определяется выражение (12). Аналогичные соображения по углам g и g₁ не отличаются от сформулированных в п.1.и п.2.

3. Предложенный подбор параметров математических моделей обеспечил полную компенсацию составляющих решения, содержащих угловые скорости дрейфа гироскопических чувствительных элементов.

4. Поскольку ошибки, поступающие на вход первого и второго интеграторов, а также возникающие в процессе интегрирования не содержат угловых скоростей дрейфа гироскопических чувствительных элементов, то и ошибки в определении приращения составляющих скорости объекта, а также ошибки в приращении координат широты и долготы, также будут свободны от угловых скоростей дрейфа чувствительных элементов.

5. Следует особо подчеркнуть, что ошибка курса объекта а определяется формулой (5) не претерпит каких-либо изменений и будет в полной мере зависеть от угловых скоростей дрейфа гироскопических чувствительных элементов.

В заключение приведем новые формулы в сравнении с формулами (5) для

 

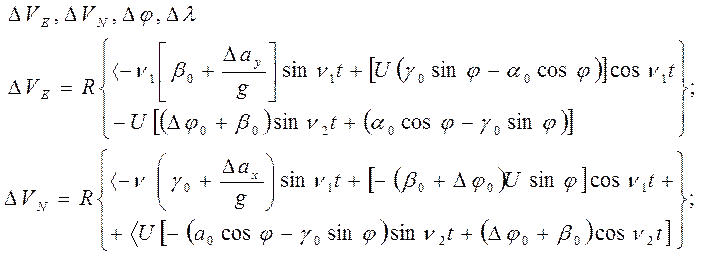
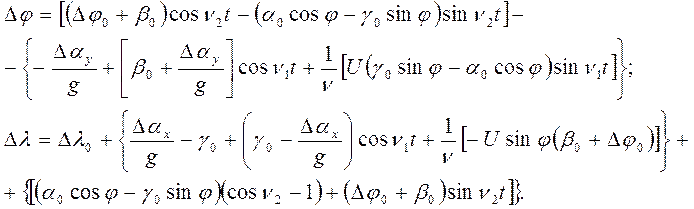
Как это вытекает из приведенных выше выражений оставшиеся ошибки в полученной информации определяется неточной начальной выставки стабилизированной платформы, неточным вводом начальной широты места объекта, а также инструментальными ошибками акселерометров.

Естественно, что никакими методами обработки информации исключить или даже уменьшить перечисленные ошибки невозможно.