Антенны типа «Волновой канал», страница 7

Подставив d_д=0,14 м; d_р=0,06 м, в (2.13), получим, что длина антенны L=0,34 м.

Коэффициент К₁ определим, используя график зависимости К₁ от ,представленный

на рисунке 2.3.

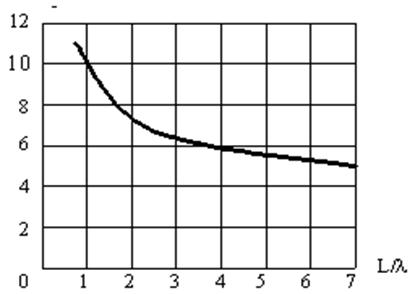
                       Рисунок 2.3 – Вспомогательный график для расчета коэффициента                                        

                                               направленного действия антенны

Так как =0,636; то К₁≈ 11. Подставив полученные численные значения в формулу (2.12), получим, что коэффициент направленного действия антенны D=6,996.

2.3 Расчёт входного сопротивления

Для расчёта входного сопротивления воспользуемся формулой:

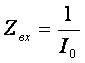                                             .                                                                (2.14)

Ток в активном вибраторе, вычисленный по формуле (1.21) I₀=1.877∙10^-3 - 8.529i∙10^-3 А, поэтому входное сопротивление антенны, рассчитанное по формуле (2.14) будет  24.611 + 111.831i Ом. Реактивная составляющая входного сопротивления не равна нулю потому, что ранее принятое собственное сопротивление активного вибратора не компенсирует наведённое сопротивление. Для получения высокого коэффициента бегущей волны необходимо равенство нулю реактивной части Z_вх. При выполнении условия

                                   X₀₀^’= −X_нав=X₀₀ – X_вх                                                          (2.15)

происходит взаимная компенсация наведенного и собственного реактивного сопротивлений. Подставив X₀₀= −10 Ом, X_вх= +111.831 Ом в формулу (2.15),

получим собственное сопротивление активного вибратора Х₀₀^’= –121,831 Ом. Таким образом Z_вх= 24,611 Ом.

 3 Определение геометрических размеров антенны. 

                   Для прямолинейного тонкого вибратора с круглым поперечным сечением и длиной, близкой к  реактивное сопротивление можно определить по формуле:

                            ,                                                                     (3.1)

где а – радиус поперечного сечения вибратора,

− укорочение или удлинение вибратора по сравнению с ,

 2l−длина вибратора.

Используя выражение (3.1) определим линейные размеры 2-х директоров. Укорочение вибратора по сравнению с  рассчитывается по формуле:    

                                                    .                                                                 (3.2)

Подставив выражение (3.2) в формулу (3.1) и выразив l,получим:

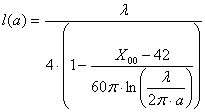                                                                                           (3.3)                   

График функции (3.3),построенный в САПР MathCAD  представлен на рисунке 3.1

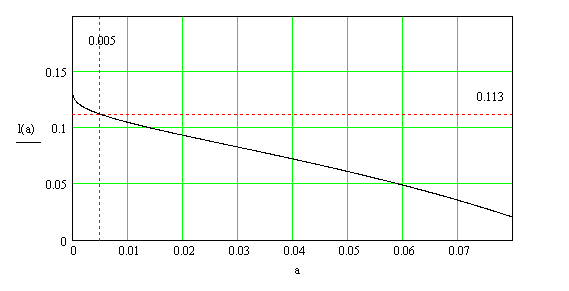
          Рисунок 3.1– График зависимости длины пассивного вибратора от радиуса

                                   поперечного сечения вибратора