Расчет антенны, предназначенной для системы спутникового телевидения, страница 5

В результате вычисления получим: см исм. Расстояние между фазовыми центрами должны удовлетворять допуску на смещение фазового центра облучателя из фокуса зеркала вдоль его оси, для этого необходимо, чтобы выполнялось условие:

.                               (13)

Подставим значения в (13) и получим, что данное условие выполняется поскольку  и .

Подставим численные значения и построим график, который приведен на рисунке 5.

Рисунок 5.Требуемая, реальная ДН облучателя в Е – плоскости и отклонение реальной ДН от требуемой.

Аналогично  и для Н - плоскости, воспользуемся формулой из [1]:

,                      (14)

где .

Рисунок 6. Требуемая, реальная ДН облучателя в Н - плоскости и отклонение реальной ДН от требуемой.

На рисунках 5 и 6  .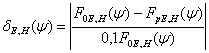

Отличие реальной ДН от требуемой ДН облучателя в обеих плоскостях не превышает 7%, а, следовательно, определенные выше размеры облучателя можно принять подходящими.

6. РАСЧЕТ РЕАЛЬНОГО РАСПРЕДЕЛЕНИЯ ПОЛЯ И ДН ЗЕРКАЛА.

Данный расчет проводится для сравнения реального  и требуемого  распределений поля в раскрыве зеркала также в двух плоскостях. Для параболоида вращения (усеченном параболоиде) с реальной нормированной ДН облучателя  справедливо . После нормировки на максимум  получим:

.                                          (15)

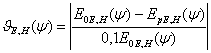Здесь величина  определятся углом  как и в выражении (3). Графики реальных  и требуемых  распределений поля в раскрыве зеркала приведены на рисунках 7 и 8. Величина  определяет отклонение реальной зависимости от требуемой.

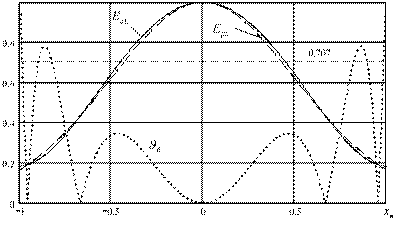
Рисунок 7.Требуемое и реальное распределение поля в Е - плоскости.

Рисунок 8.Требуемое и реальное распределение поля в Н - плоскости.

Наконец рассчитаем ДН антенны  в главных плоскостях пользуясь формулами из [1]. Запишем выражение нормированной ДН антенны в Е - плоскости:

,                                                 (16)

где ; ; ;

Аналогичным образом для Н - плоскости:

,                                                (17)

где .