Расчет значений k0 и e в уравнении аррениуса с использованием метода наименьших квадратов и поиска решения excel. Расчет значений константы равновесия с использованием метода наименьших квадратов

2. расчетная часть

2.1. расчет значений k₀ и e в уравнении аррениуса с использованием метода наименьших квадратов и поиска решения excel

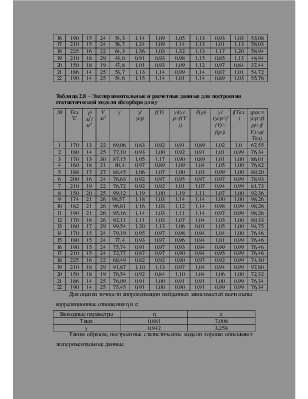
Для расчета K₀ и E в уравнении Аррениуса

K = K₀*e^-E/RT

Использован метод наименьших квадратов. Вычисления проведены в Microsoft Excel:

                                                                                                                                                                      Таблица 2.1 - Зависимость константы скорости от температуры

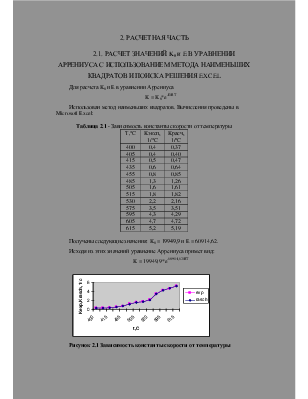
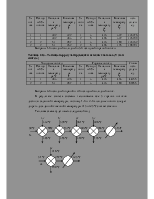
Получены следующие значения: K₀ = 19949,9 и E = 60914,62.

Исходя из этих значений уравнение Аррениуса примет вид:

K = 19949,9*e^-60914,62/RT

Рисунок 2.1 Зависимость константы скорости от температуры

 

2.2 расчет значений константы равновесия с использованием метода наименьших квадратов

Общий вид зависимости константы равновесия от температуры:

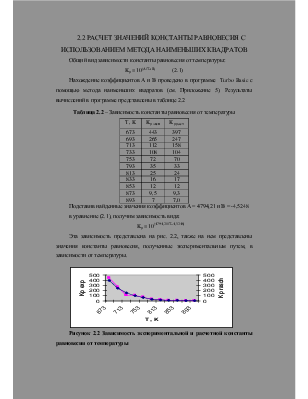
K_р = 10^(A/T+B)            (2.1)

Нахождение коэффициентов А и В проведено в программе  Turbo Basic с помощью метода наименьших квадратов (см. Приложение 5). Результаты вычислений в программе представлены в таблице 2.2

Таблица 2.2 – Зависимость константы равновесия от температуры

Подставив найденные значения коэффициентов А = 4794,21 и В = -4,5248

в уравнение (2.1), получим зависимость вида:

K_р = 10^{(4794,21/T–4,5248)}

Эта зависимость представлена на рис. 2.2, также на нем представлены значения константы равновесия, полученные экспериментальным путем, в зависимости от температуры.

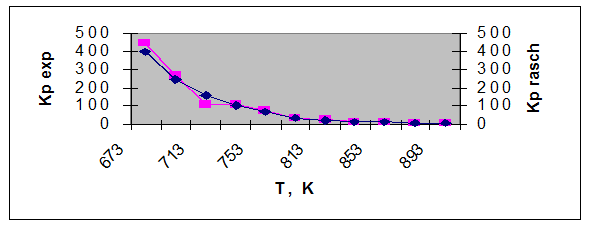Рисунок 2.2 Зависимость экспериментальной и расчетной константы равновесия от температуры

2.3 Расчет статистической модели абсорбера методом брандона

Влияющие факторы:

Tвх - температура на входе в абсорбер, °C;

r - плотность орошения, м³/м²;

V - объем, м³

Выходные параметры:

Tвых - температура на выходе из абсорбера, °C;

y - степень абсорбции, %

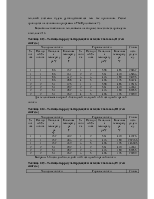
Экспериментальные данные для построения статистической модели абсорбера приведены в Приложении 1.

Первым этапом решения данной задачи является ранжирование влияющих факторов. Все этапы построения модели абсорбера проведены для каждого выходного параметра в отдельности.

Ø  Построение матрицы коэффициентов парной корреляции

Элементами матрицы являются коэффициенты парной корреляции. Полученная матрица коэффициентов парной корреляции приведена в таблице 2.3 и таблице 2.4.

Таблица 2.3 – Матрица парных коэффициентов корреляции для Tвых

	Tвх	r	V	Tвых
Tвх	1	-0,1048	0,0264	0,5386
r	-0,1048	1	0,0252	-0,7152
V	0,0264	0,0252	1	-0,5229
Tвых	0,5386	-0,7152	-0,5229	1

Таблица 2.4 – Матрица парных коэффициентов корреляции для y

	Tвх	r	V	y
Tвх	1	-0,1048	0,0264	-0,3797
r	-0,1048	1	0,0252	0,6967
V	0,0264	0,0252	1	0,6517
y	-0,3797	0,6967	0,6517	1

Ø  Вычисление частных коэффициентов множественной корреляции

Полученные частные коэффициенты для каждого из выходных параметров приведены в таблице 2.5.

Таблица 2.5

Выходные параметры	Влияющие факторы
	Tвх	r	V
Tвых	0,9961	0,9978	-0,9966
y	-0,9759	-0,9936	0,9936

Ø  Ранжирование факторов

В соответствии с убыванием величины частных коэффициентов корреляции определим порядок расположения влияющих факторов в уравнении (1.6) для выходных параметров:

Таблица 2.6

Tвых	1	r	x2	y	1	V	x3
	2	V	x3		2	r	x2
	3	Tвх	x1		3	Tвх	x1