Принимаем
сечение стойки состоящим из 6 слоёв досок толщиной 33 мм (после острожки досок толщиной 40 мм), тогда ![]() мм. Ширину сечения
колонны принимаем равной
мм. Ширину сечения
колонны принимаем равной ![]() мм (после острожки
боковых поверхностей колонны, склеенной из досок шириной 175 мм). Нагрузка от собственного веса стойки:
мм (после острожки
боковых поверхностей колонны, склеенной из досок шириной 175 мм). Нагрузка от собственного веса стойки:
![]() кН/м,
кН/м,
где ![]() кН/м3
– объёмный вес древесины сосны;
кН/м3
– объёмный вес древесины сосны; ![]() – коэффициент
надёжности по нагрузке.
– коэффициент
надёжности по нагрузке.
Расчётная нагрузка от стенового ограждения, распределённая по вертикали, с учётом элементов крепления (15 % от веса стенового ограждения):
![]() кН/м.
кН/м.
Эксцентриситет
приложения нагрузки от стены ![]() на стойку принимаем
равным половине суммы высот сечений стены и стойки:
на стойку принимаем
равным половине суммы высот сечений стены и стойки:
![]() м.
м.
Определение внутренних усилий в стойке
Изгибающий момент, действующий на фахверк от веса стен:
![]() кНм.
кНм.
Изгибающий момент, действующий на фахверк от ветровой нагрузки:
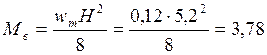 кНм.
кНм.
Полный изгибающий момент, действующий в расчётном сечении фахверка:
![]() кНм.
кНм.
Продольная сила, действующая в расчётном сечении фахверка, будет складываться из двух составляющих: собственного веса фахверка и веса стенового покрытия:
![]() кН.
кН.
Конструктивный расчёт
Фахверк работает как шарнирно закреплённый стержень в условиях сжатия с изгибом.
Определим характеристики сечения:
![]() м2.
м2.
Момент инерции сечения:
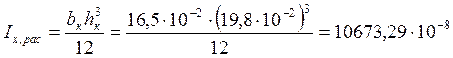 м4.
м4.
Момент сопротивления сечения равняется:
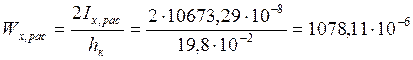 м3.
м3.
Определим расчётную длину в плоскости рамы:
![]() м.
м.
где ![]() –
коэффициент, равный 1 при обоих шарнирно закреплённых концах по СНиП II-25-80 п.4.21.
–
коэффициент, равный 1 при обоих шарнирно закреплённых концах по СНиП II-25-80 п.4.21.
В плоскости действия ветровой нагрузки расчёт фахверка производится как сжато-изгибаемого элемента. Определим его гибкость в плоскости изгиба (для прямоугольного сечения).
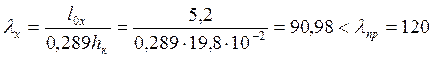
Определим
коэффициент ![]() по формуле № 8 СНиП II-25-80:
по формуле № 8 СНиП II-25-80:
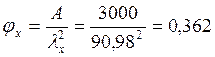 ,
,
где ![]() –
коэффициент для древесины равный 3000.
–
коэффициент для древесины равный 3000.
Определим
коэффициент ![]() по формуле № 30 СНиП II-25-80:
по формуле № 30 СНиП II-25-80:
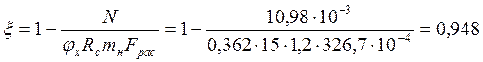 ,
,
где
![]() МПа – расчётное сопротивление древесины
2-го сорта;
МПа – расчётное сопротивление древесины
2-го сорта; ![]() – коэффициент условий работы, равный 1,2 и
учитываемый при расчёте конструкций с учётом воздействия кратковременных
нагрузок (ветровая) по таблице № 6 СНиП II-25-80.
– коэффициент условий работы, равный 1,2 и
учитываемый при расчёте конструкций с учётом воздействия кратковременных
нагрузок (ветровая) по таблице № 6 СНиП II-25-80.
Определим изгибающий момент от действия поперечных и продольных нагрузок по формуле № 29 СНиП II-25-80:
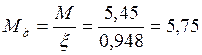 кНм.
кНм.
Расчёт фахверка на прочность произведём по формуле № 28 СНиП II-25-80:
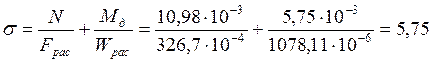 МПа
МПа![]() МПа.
МПа.
Из плоскости рамы колонну рассчитаем как центрально-сжатый элемент. Определим гибкость фахверка из плоскости изгиба:
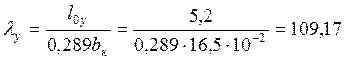 .
.
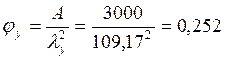 .
.
Проверим устойчивость колонны из плоскости рамы по формуле № 6 СНиП II-25-80:
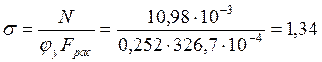 МПа
МПа![]() МПа.
МПа.
Поверку устойчивости плоской формы деформирования выполним по формуле № 33 СНиП II-25-80:
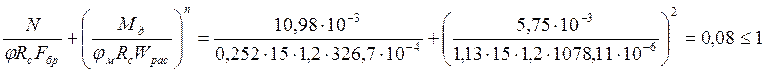 ,
,
где ![]() –
коэффициент, равный 2 для элементов без закрепления растянутой зоны из
плоскости деформирования;
–
коэффициент, равный 2 для элементов без закрепления растянутой зоны из
плоскости деформирования; ![]() – коэффициент,
определяемый по формуле № 23 СНиП II-25-80:
– коэффициент,
определяемый по формуле № 23 СНиП II-25-80:
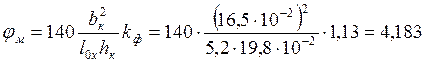 ,
,
где ![]() –
коэффициент, зависящий от формы эпюры изгибающих моментов на участке
–
коэффициент, зависящий от формы эпюры изгибающих моментов на участке ![]() , принимаемый по таблице № 2 приложения № 4
СНиП II-25-80.
, принимаемый по таблице № 2 приложения № 4
СНиП II-25-80.
Следовательно, устойчивость фахверка обеспечена.
Список используемой литературы
1. СНиП II-25-80 “Деревянные конструкции”.
2. СНиП 2.01.07-85* “Нагрузки и воздействия”.
3. СНиП II-23-81* “Стальные конструкции”.
4. “Индустриальные деревянные конструкции. Примеры проектирования”: Учеб. пособие для ВУЗов / Ю.В. Слицкоухов, И.М. Гуськов, Л.К. Ермоленко и др.; под ред. Ю.В. Слицкоухов. – М.: Стройиздат, 1991. – 256 с.
5. Г.Г. Карлсен, М.Е. Каган, Г.В. Свенцицкий, Б.А. Освенский, Ю.В. Слицкоухов “Индустриальные деревянные конструкции. Примеры проектирования”: Под ред. Г.Г. Карлсена. – М.: Издательство литературы по строительству, 1967. – 320 с.
6. Шишкин В.Е. “Примеры расчёта конструкций из дерева и пластмисс”: Учеб. Пособие для техникумов – М.: Стройиздат, 1974. – 219 с.
7. П.А. Дмитриев “Деревянные балки и балочные клетки”. 1989. – 160 с.
8. М.М. Гапоев, И.М. Гуськов, Л.К. Ермоленко, В.И. Линьков, Е.Т. Серова, Б.А. Степанова, Э.В. Филимонов “Конструкции из дерева и пластмасс”: Учебник. – М.: Издательство АСВ, 2004. – 440 с.
9. “Конструкции из дерева и пластмасс”: В.А. Иванов, В.З. Клименко. – Киев: Вища школа. Головное издательство, 1983. – 279 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.