![]() кН.
кН.
Расчётные усилия в элементах фермы определяются методом вырезания узлов.
Расчётные усилия в элементах фермы приведены в таблице № 2.
Таблица 3 Усилия в элементах фермы
|
Элементы фермы и опорные реакции |
Стержни |
Усилия от первого варианта загружения, кН |
Усилия от второго варианта загружения, кН |
Расчётные усилия, кН |
|
Верхний пояс |
AC |
-29,6 |
-29,6 |
29,6 |
|
BC |
-29,6 |
-29,6 |
29,6 |
|
|
Нижний пояс |
AD |
+27,47 |
+27,47 |
27,47 |
|
BD |
+27,47 |
+27,47 |
27,47 |
|
|
Стойка |
CD |
0 |
0 |
0 |
|
Элементы фермы и опорные реакции |
Стержни |
Усилия от первого варианта загружения, кН |
Усилия от второго варианта загружения, кН |
Расчётные усилия, кН |
|
Опорные реакции |
VA |
21,98 |
20,48 |
|
|
VB |
21,98 |
23,48 |
Подбор сечений элементов фермы
Расчёт верхнего пояса.
Максимальный изгибающий момент в панели AC (BC) от внеузловой равномерно распределённой нагрузки определяем для второго варианта загружения с учётом того, что на верхний пояс приходится половина собственного веса фермы:
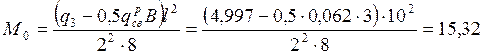 кНм.
кНм.
Верхний пояс
проектируем из бруса сечением ![]() мм после острожки (
мм после острожки (![]() мм).
мм).
Для уменьшения изгибающего момента в панели фермы создаём внецентренное приложение продольного сжимающего усилия, в результате чего в узлах верхнего пояса возникают разгружающие отрицательные моменты.

Рис. 7
Расчётный эксцентриситет
определяем из условия соединения верхнего и нижнего поясов на лобовой врубке
(примем глубину врубки ![]() м):
м):
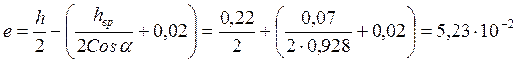 м.
м.
Тогда разгружающий момент будет равен:
![]() кНм.
кНм.
Характеристики сечения в плоскости фермы: площадь поперечного сечения:
![]() м2.
м2.
Момент инерции сечения:
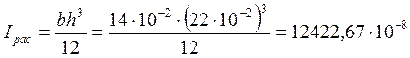 м4.
м4.
Момент сопротивления сечения равняется:
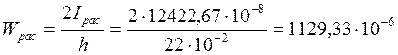 м3.
м3.
Гибкость верхнего пояса равна (для прямоугольного сечения):
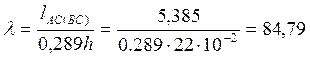 ,
,
где ![]() м –
расчётная длина элемента AC (BC).
м –
расчётная длина элемента AC (BC).
Расчёт на прочность верхнего пояса производим как сжато-изгибаемого элемента по формуле № 28 СНиП II-25-80:
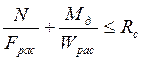 ,
,
где ![]() МПа –
расчётное сопротивление древесины 2-го сорта для здания II
класса ответственности;
МПа –
расчётное сопротивление древесины 2-го сорта для здания II
класса ответственности; ![]() – изгибающий момент от
действия поперечных и продольных нагрузок, определяемый из расчёта по
деформированной схеме.
– изгибающий момент от
действия поперечных и продольных нагрузок, определяемый из расчёта по
деформированной схеме.
Для
шарнирно-опертых элементов при симметричных эпюрах изгибающих моментов параболического
очертания ![]() следует определять по формуле:
следует определять по формуле:
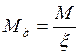 ,
,
где ![]() –
изгибающий момент в расчетном сечении без учета дополнительного момента от продольной
силы;
–
изгибающий момент в расчетном сечении без учета дополнительного момента от продольной
силы; ![]() – коэффициент, изменяющийся от 1 до 0,
учитывающий дополнительный момент от продольной силы вследствие прогиба
элемента, определяемый по формуле:
– коэффициент, изменяющийся от 1 до 0,
учитывающий дополнительный момент от продольной силы вследствие прогиба
элемента, определяемый по формуле:
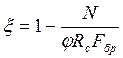 ,
,
где ![]() –
коэффициент, определяемый по формуле № 8 СНиП II-25-80
(для
–
коэффициент, определяемый по формуле № 8 СНиП II-25-80
(для ![]() ). В случаях, когда в шарнирно-опертых
элементах эпюры изгибающих моментов имеют прямоугольное очертание, коэффициент
). В случаях, когда в шарнирно-опертых
элементах эпюры изгибающих моментов имеют прямоугольное очертание, коэффициент ![]() следует умножать на поправочный коэффициент
следует умножать на поправочный коэффициент
![]() :
:
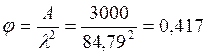 ,
,
где ![]() –
коэффициент для древесины равный 3000.
–
коэффициент для древесины равный 3000.
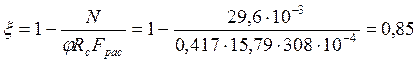 .
.
![]() ,
,
где ![]() –
коэффициент, который следует принимать равным 0,81 при эпюрах прямоугольного
очертания (от постоянного изгибающего момента
–
коэффициент, который следует принимать равным 0,81 при эпюрах прямоугольного
очертания (от постоянного изгибающего момента ![]() ).
).
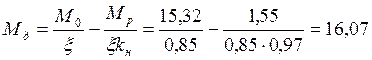 кНм.
кНм.
Расчётное напряжение в панели BC (AC):
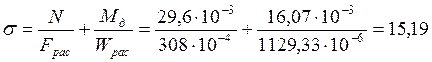 МПа
МПа![]() МПа.
МПа.
Условие прочности выполняется.
Прогиб панели AC (BC) в середине пролёта:
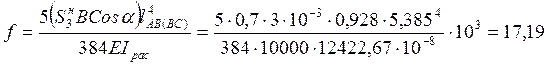 мм
мм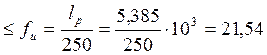 мм,
мм,
где ![]() МПа –
модуль упругости древесины.
МПа –
модуль упругости древесины.
Условие дефомативности выполняется.
Проверим панель AC (BC) на устойчивость из плоскости фермы по формуле № 6 СНиП II-25-80:
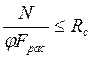 .
.
Характеристики сечения из плоскости фермы: момент инерции сечения:
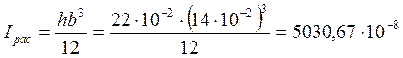 м4.
м4.
Момент сопротивления сечения равняется:
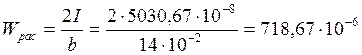 м3.
м3.
Гибкость верхнего пояса равна (для прямоугольного сечения):
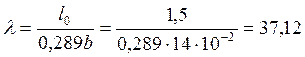 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.