Основы планирования экстремального эксперимента для оптимизации многофакторных технологических процессов, страница 4

Величина t-критерия сравнивается с табличным значением, число степеней свободы N(n-1) (Приложение, табл. 2). Можно также определять доверительный интервал для коэффициентов регрессии: . Если абсолютное значение доверительного интервала превышает величину коэффициента регрессии, гипотеза о незначимости коэффициента может быть принята.

Рассмотрим еще один пример. Условия и результаты исследования выхода в процентах (у) редкого металла из руды в зависимости от концентрации кислоты (, г/моль) представлены в табл. 3.

Таблица 3

Условия и результаты исследования выхода редкого металла из руды

 и  обозначают параллельные опыты,  - их среднее значение:

Уравнение регрессии:

.

Рассчитаем дисперсию каждого опыта и дисперсию всего эксперимента:

, , .

Критерий Кохрена:

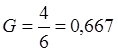, f₁ = 1, N = 3.

Табличное значение критерия Кохрена составляет 0,966, поэтому можно принять гипотезу об однородности дисперсий.

Дисперсия эксперимента:

.

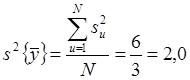Для случая двух параллельных определений можно использовать формулу:

,

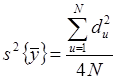где d_u - разность между параллельными определениями.

Оценим значимость коэффициентов регрессии. Дисперсии коэффициентов: 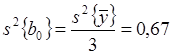, 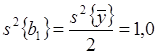. Величины t-критерия равны 25,6 и 6,0 соответственно, число степеней свободы f = N(n-1) = 3. Табличная величина t-критерия для 5%-ного уровня значимости и трех степеней свободы равна 3,18. Итак, гипотеза о значимости коэффициентов регрессии может быть признана.

Из расчета остаточной суммы квадратов , , ,  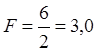со степенями свободы 1 для числителя и N(n-1) = 3 для знаменателя. Табличное значение критерия Фишера для 5%-ного уровня значимости F(0,05, f₁, f₂) = F(0,05, 1; 3) = 10,1, гипотеза адекватности уравнения регрессии может быть принята.

Еще одной важной характеристикой в регрессионном анализе является дисперсия предсказанного значения регрессионной функции , показывающая точность предсказания у в диапазоне изменения независимой переменной. В случае линейной модели:

.

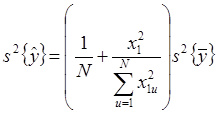Дисперсия предсказанного значения минимальна в центре эксперимента и максимальна на его границе. Для рассматриваемого примера максимальная дисперсия равна:

.

Доверительный интервал для граничных значений зависимой переменной: .

Если линейное уравнение неадекватно, переходят к представлению результатов полиномом второго порядка:

.

Формулы для расчета коэффициентов регрессии, ошибок и дисперсии предсказанного значения (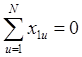) имеют следующий вид:

,

,

, ,

, ,

,

.

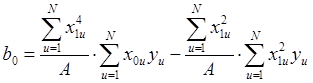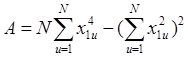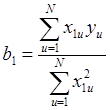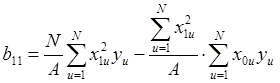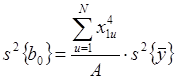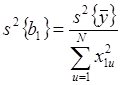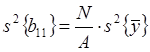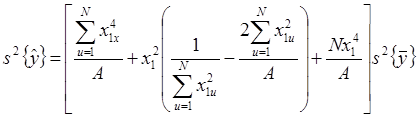Оптимизация процессов включает этап получения модели с несколькими независимыми переменными. На этом этапе уже используется многомерный регрессионный анализ. Задача формулируется так: найти коэффициенты уравнения регрессии степени d с x₁, x₂… x_k независимыми переменными по результатам N опытов. Число коэффициентов регрессии равно  и необходимое условие: . Если соблюдается ортогональность вектор-столбцов матрицы независимых переменных (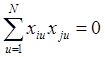, , , ), то коэффициенты регрессии и их ошибки также определяются независимо друг от друга по уже известным формулам:

, , .

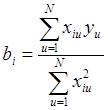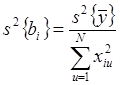Статистический анализ уравнения регрессии аналогичен однофакторному.

В метод Бокса-Уильсона входит, как составная часть, один из методов планирования эксперимента - метод факторного планирования. Он также дает возможность получать модели, связывающие зависимую и независимые переменные.