Основы планирования экстремального эксперимента для оптимизации многофакторных технологических процессов, страница 2

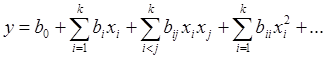
Коэффициенты полиномов рассчитывают по результатам эксперимента. На первом этапе, в крутом восхождении, обычно используют полиномы первого порядка. Оценка коэффициентов полинома - задача регрессионного анализа, одного из разделов математической статистики. Этот раздел математической статистики имеет самостоятельное значение, поэтому рассмотрим его в связи с задачей достижения оптимума.

Регрессионный анализ

Рассмотрим самый простой случай: Т результатов наблюдений параметра оптимизации y, зависящих от значений независимой переменной x₁, необходимо представить полиномом первого порядка:

y = b₀ + b₁x₁.

Это уравнение называют уравнением регрессии, в котором b₀, b₁ - коэффициенты регрессии.

В математической статистике при обработке результатов экспериментов последние рассматривают как случайную выборку из неограниченно большого числа наблюдений, или, как говорят, из гипотетической генеральной совокупности по результатам выборки, учитывая неопределенность, обусловленную ограниченностью экспериментального материала. По традиции греческими буквами обозначают параметры генеральной совокупности, латинскими - их выборочные оценки. Уравнение регрессии для генеральной совокупности имеет вид:

.

Где b₀ - оценка b₀;

       b₁ - оценка b₁;

       y - оценка h.

          b₀ ® b₀, b₁ ® b₁, y ® h.

Регрессионный анализ применим при выполнении следующих предпосылок: ошибки в определении х₁ малы по сравнению с ошибкой у, дисперсии зависимой переменной для разных опытов однородны (они являются оценками одной и той же дисперсии генеральной совокупности s² {y}), значения у - независимые, нормально распределенные случайные величины.

Рассмотрим определение коэффициентов регрессии с помощью методов наименьших квадратов.

Уравнение регрессии для всей совокупности N опытов имеет вид:

,

где u - номер опыта (изменяется от 1 до N).

Необходимо найти значения b₀ и b₁, которые некоторым наилучшим образом представляли бы результаты эксперимента.

Если определять оценки коэффициентов регрессии из условия:

,

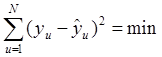где - рассчитанные по уравнению значения зависимой переменной, а - экспериментальные значения, то они обладают некоторыми оптимальными в статистическом смысле свойствами: состоятельностью, несмещенностью, эффективностью и достаточностью. Оценка параметра состоятельна - если она при увеличении объема выборки приближается к истинному значению параметра; несмещена - если математическое ожидание ее равно оцениваемому параметру; эффективна - если оценка характеризуется минимальной дисперсией; достаточна - если включает максимум информации о параметре.

Сумму квадратов отклонений можно представить так:

.

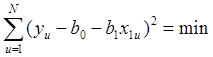Для определения минимума:

,

.

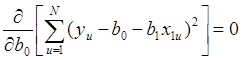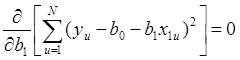После проведения простых операций можно записать:

,

.

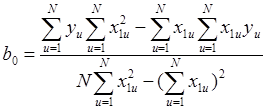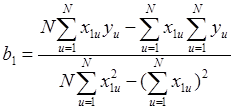Формулы для расчета коэффициентов регрессии упрощаются, если заранее планировать эксперимент, располагая опыты симметрично относительно среднего значения независимой переменной.

Удобно значения независимой переменной в натуральном масштабе  заменять кодированные (х) в интервале -1, +1. Для кодирования пользуются формулой:

,

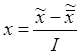где - кодированное значение переменной;

      - натуральное значение переменной;

      I - интервал варьирования,

, .

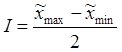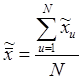В планировании эксперимента различные значения, которые принимает независимая переменная , называются уровнями, - основным (нулевым) уровнем,  - нижним уровнем. Благодаря симметричному расположению опытов .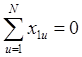

Коэффициенты регрессии в этом случае рассчитываются по формулам:

, .

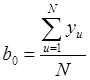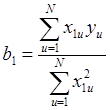Рассмотрим пример определения коэффициентов.