Министерство общего образования Российской Федерации
Санкт-Петербургский государственный технологический институт
(технический университет)
“Внутренние силовые факторы в элементах химического оборудования”.
Выполнил: ст. 823 гр. Сопыгин А. И.
Проверил: преп. Павлова Э. А.
Санкт-Петербург
2004г.
Оглавление.
стр.
1. Введение. 3
2. Расчётная часть. 4
3. Вывод. 6
4. Литература. 6
1. Введение.
В процессе эксплуатации аппаратов и машин химических производств их элементы подвергаются воздействию различных внешних сил. Для обеспечения нормальной работы конструкции эти элементы должны быть спроектированы с учётом ряда критериев работоспособности, среди которых важнейшими являются прочность, жёсткость, устойчивость.
Выбор расчётной схемы связан с упрощением системы сил, приложенных к элементу конструкции, геометрии реального объекта и схематизацией свойств материала.
Основным упрощающим приёмом в прикладной механике является приведение геометрической формы тела к схеме бруса или оболочки. Брусом, или стержнем, называется тело, один размер которого значительно больше двух других. Оболочкой называется тело, один размер которого значительно меньше двух других. Если срединная поверхность оболочки представляет собой плоскость, то такая оболочка называется пластиной. Массивным называется тело, у которого все три размера – величины одного порядка.
Линия, соединяющая центры тяжести последовательно выбранных сечений стержня, называется его осью. Поперечным называют сечение, перпендикулярное к оси стержня.
Приложенные к телу силы, вызванные действием других тел, называют внешними силами.
Сопротивление тел, оказываемое действующим на них внешним нагрузкам, обусловливается наличием в этих телах внутренних сил, природа которых объясняется теорией строения материи.
Внутренние усилия определяются с помощью метода сечений, сущность которого состоит в следующем:
а) изучаемый стержень мысленно рассекается плоскостью, перпендикулярной к его оси, на две части;
б) отбрасывается одна из частей стержня (обычно наиболее нагруженная);
в) действие отброшенной части на оставшуюся заменяется внутренними усилиями, приведение которых к центру тяжести сечения по правилам статики даёт в общем случае главный вектор V и главный момент М;
г) для рассматриваемой части стержня составляются уравнения равновесия, из которых определяются составляющие главного вектора N, Qy, Qx и главного момента Т, Мy и Мz.
К простым видам деформаций относятся:
1. Растяжение или сжатие – вид нагружения стержня, при котором внутренние усилия в поперечных сечениях приводятся к силе, направленной по оси стержня.
2. Кручение – вид нагружения, при котором внутренние усилия приводятся к паре сил, действующей в плоскости, перпендикулярной к оси стержня. При кручении отличен от нуля только крутящий момент Т.
3. При действии в сечении поперечных сил Qy или Qz и отсутствии других силовых факторов имеет место сдвиг.
4. Чистым плоским изгибом называют вид нагружения, при котором внутренние усилия приводятся к паре, действующей в плоскости, совпадающей с одной из главных осей (обычно осью симметрии) поперечного сечения и осью стержня.
К простым видам деформаций относятся также и плоский поперечный изгиб – вид нагружения стержня, при котором внутренние усилия приводятся к паре, распложенной в главной плоскости инерции, и силе, действующей по линии пересечения этой плоскости с поперечным сечением стержня.
Для стержней в общем случае величина внутреннего усилия переменна по длине. Графическое изображение изменения внутреннего усилия в зависимости от координаты x по длине стержня называют эпюрой соответствующего внутреннего усилия. Изучение эпюры позволяет определить положение опасного сечения, а координаты эпюры, показывающие величину внутреннего усилия, дают возможность выполнить расчёт по соответствующему критерию работоспособности.
Грузовым участком называется часть длины стержня, на протяжении которой действует один и тот же непрерывный закон изменения внутреннего усилия.
2. Расчётная часть.
Задача №1.
I участок: 0м≤x1≤3м.
ΣX=0;
Qx+F1=0;
Qx=-F1=-30 кН.
II участок: 3м≤x2≤7м.
Qx+F1+F2=0;
Qx=-F1-F2=-30-40=-70 кН.
III участок: 7м≤x3≤9м.
Qx+F1+F2-F3=0;
Qx=-F1-F2+F3=-30-40+90=20 кН.
Задача №2.
I участок: 0м≤x1≤3м.
T0-T3=0;
T0=T3=30 кН·м.
II участок: 3м≤x2≤7м.
T0-T3+T2=0;
T0=T2-T3=30-90=-60 кН·м.
III участок: 7м≤x3≤9м.
T0-T3+T2-T1=0;
T0=T3-T2+T1=30-90+70=10 кН·м.
Задача №3.
I участок: 0м≤x1≤4м.
Qx=-F1+q1·x1;
Qx=0=-30+5·0=-30 кН;
Qx=4=-30+5·4=-10 кН;
Mx=F1·x-(q1·x2)/2;
Mx=0=-30·0-(5·02)/2=0 кН·м;
Mx=4=-30·4-(5·42)/2=80 кН·м;
II участок: 4м≤x2≤6м.
Qx=-F1+(q1·l22)/2;
Qx=4=Qx=6=-30+(5·42)/2=10 кН;
Mx=F1·x-q1·l2·(x2-l2/2)+M1;
Mx=4=30·4-5·4·(4-4/2)+70=150 кН·м;
Mx=6=30·6-5·4(6-4/2)+70=170 кН·м;
Задача №4.
ΣMA=0;
RB·(l1+l2+l3)-q2·l3·(l1+l2+l3/2)-F2·l1+M2=0;
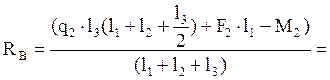
 кН.
кН.
ΣMB=0;
-RA·(l1+l2+l3)+M2+F2·(l2+l3)+q2·l32/2=0;
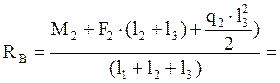
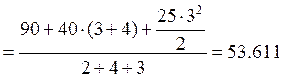 кН.
кН.
Проверка:
RA-F2-q2·l3+RB=0;
53.611-40-25·3+61.388=0;
0=0;
I участок: 0м≤x1≤2м.
Qx=RA;
Qx=0=Qx=2=53.611 кН;
Mx=-M2+RA·x1;
Mx=0=-90+53.611·0=-90 кН·м;
Mx=2=-90+53.611·2=17.222 кН·м;
II участок: 2м≤x2≤6м.
Qx=RA-F2;
Qx=2=Qx=6=53.611-40=13.611 кН;
Mx=-M2+RA·x2-F2·(x2-l1);
Mx=2=-90+53.611·2-40·(2-2)=17.222 кН·м;
Mx=6=-90+53.611·6-40·(6-2)=71.66 кН·м;
III участок: 0м≤x3≤3м.
Qx=-RB+q2·x3;
Qx=0=-61.388+25·0=-61.388 кН;
Qx=3=-61.388+25·3=13.611 кН;
Qx=-RB+q2·x0=0; x0=RB/q2=61.388/25=2.455м;
Mx=RB·x3-q2·x32/2;
Mx=0=61.388·0-25·02/2=0 кН·м;
Mx=3=61.388·3-25·32/2=75,66 кН·м;
Mx=x0=61.388·2.455-25·2.4552/2=75.37 кН·м;
3. Вывод.
Для первой задачи опасным сечением является сечение в точке, где приложена сила растяжения F1=90кН.
Для второй задачи опасным сечением является сечение в точке приложения крутящего момента T2=90кН·м.
Для третьей задачи опасным сечением является сечение в точке, где приложен изгибающий момент M1=70кН·м.
Для четвёртой задачи опасным сечением является сечение в точке, где приложена сила F2=40кН.
4. Литература.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.