19. Алгоритмы поиска с помощью деревьев.
Идеально сбалансированные деревья.
При использовании, в целях поиска элементов данных, по значению двоичного ключа, используют дерево двоичного поиска. Вершина дерева больше ключа её левого поддерева, а правого меньше. Дерево с новым ключом вершины обозначим x, по правилам пишется листовая вершина, в которой находился бы этот ключ, если бы он входил в это дерево. Ситуации: 1) Такая вершина не существует. 2) Вершина существует и уже занята каким-нибудь ключом «y». Если x>y, то ключ x заносится в листовую вершину у правого поддерева. Если x<y, то ключ x заносится в левое поддерево. Исключение: При выполнении исключения ключа из дерева сначала происходит поиск ключа, затем: 1) Ключ содержится в листовой вершине, у отца которого имеется два сына. 2) У предка один сын (любой). 3) Ключ содержится во внутренней вершине (имеет одного потомка). 4) Внутренняя вершина (имеет два потомка); У левого потомка, правый путь.
Сбалансированные деревья. АВЛ - деревья.
h-высота дерева; Т-дерево; Т0-пустое дерево; Т1-дерево с одной вершиной; Тh строится в виде корня левого потомка Т(h-1), а правого Т(h-2). Деревья Фебоначо: 1) Пустое дерево – есть дерево Фебоначо с высотой 0. 2) Единая вершина – есть дерево Фебоначо с высотой 1
3) Если дерево с высотой (h-1) и дерево (h-2) являются деревьями Фебоначо, а x-новый корень дерева, то Th=<T(h-1),x,T(h-2)> 4) Других деревьев Фебоначо нет. Число вершин в дереве Th определяется из следующего: N0=0, N1=1, Nh=N(h-1)+1+N(h-2). Эти числа иначе называют числами Леонардо. r - корневая вершина, L-левое поддерево, R-правое поддерево, hl-высота L, hr-высота R. Если hl:=hl+1: 1) hl=hr, сбалансированность остаётся. 2) hl>hr, сбалансированность улучшается. 3) hl<hr, требуется перестройка.
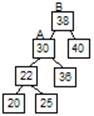
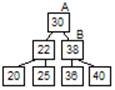
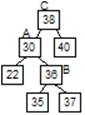
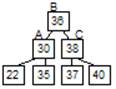
Количество операций ≈ log n
Деревья оптимального поиска.
Поиск похожих элементов с разной вероятностью. Пусть дерево поиска П количество вершин, i-вершина, pi-вероятность обращения. Организация дерева таким образом, чтоб обеспечить min количество шагов с большим количеством обращений.
Корень дерева имеет высоту 1. pi*hi – сумма произведений должна быть min, hi-длина пути к вершине. 1,2,3 – обращения. 1/7, 2/7, 4/7 – вероятность.
1 сл. 2 сл. 3 сл. 4 сл. 5 сл.
![]()
![]()
![]()
![]()
P(1)=1*4/7+2*2/7+3*1/7=11/7 P(2)=12/7 P(3)=13/7 P(4)=15/7 P(5)=17/7
Сложность алгоритма поиска составляет n2, n-количество вершин n*log n.
Деревья цифрового поиска.
В каждой вершине такого дерева хранится полный ключ, но переход по левой или правой ветви происходит, не путём сравнения ключа элемента со значением других ключей, а на основе очередного бита аргумента. Если содержащийся в корневой вершине ключ не совпадает с аргументом ключа, то сравнивается с самым левым ключом, если ключ=0, то переход по левой ветви, а 1, то по правой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.