Решения экзаменационных заданий по дисциплине "Высшая математика", страница 2

№5. Первый замечательный предел с выводом.

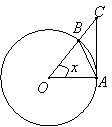Предположим, что угол x заключен в границах . Рассмотрим окружность единичного радиуса 1 и проведем некоторые построения.

Из рисунка видно, что площ.площади сект АОВ < площ. . Так как указанные площади равны соответственно , то .

Разделив все члены этого неравенства на , получим

       (1)

Неравенство (1) доказано для , но оно верно и для , т.к.

Ф-я  непрерывна в любой () x, в частности, в () x=0, так что  Т.о., обе ф-ии  имеют в точке  предел равный единице.