Расчет антенны, предназначенной для радиотелескопа, страница 3

Значения коэффициентов пропорциональности  выбираются из таблиц, приведенных в [5, стр. 28]. Точное значение коэффициента для Н- плоскости определяется по зависимости . Она приведена на рис.2.3.

Подставив значения в (3) получим:  см, см.

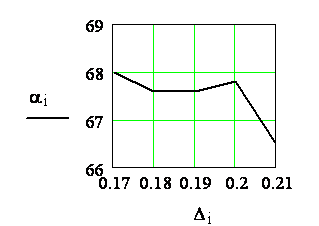
Рис. 2.3 Зависимость  от скачка поля в Н – плоскости

3 рАСЧЕТ ПАРАМЕТРОВ ОБЛУЧАТЕЛЯ АНТЕННЫ

3.1 Расчет ДН облучателя

Распределение поля в раскрыве зеркала легче всего определить методом геометрической оптики. В параболоиде вращения (или усеченном параболоиде вращения) облучатель должен создавать сферическую волну. У такой волны амплитуда убывает с удалением  от источника (облучателя) обратно пропорционально  (в дальней зоне, в среде без потерь). После отражения от зеркала фронт волны становится плоским, а амплитуда плоской волны в среде без потерь не зависит от расстояния.

Поэтому можно записать связь ДН облучателя  и поля в раскрыве  в виде  (с точностью до постоянного размерного множителя). Нормируя ДН на максимум , получим расчетную формулу для нормированной ДН облучателя (по напряженности) в Н- и Е - плоскостях:

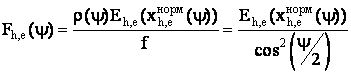,                           (4)

где нормированная координата:

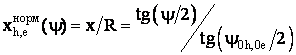.                                (4')

Для этого следует задаться углом . Его можно выбирать вблизи оптимального значения, пользуясь рис. 1.6 из [4]. Обычно значение  выбирают ориентировочно в пределах . Выбор наиболее оптимального угла раскрыва  в дальнейшем дает возможность достижения высокого КИП (коэффициента использования поверхности) при сравнительно небольших размерах облучателя и, как следствие, с меньшим затенением зеркала. Задавшись углом раскрыва  в Е - плоскости, рассчитаем ДН облучателя.

ДН облучателя в Е - плоскости будет рассчитываться по формуле:

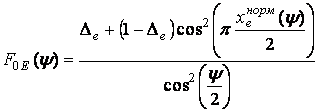,                          (5)

График нормированной ДН облучателя в Е - плоскости приведен на рис. 3.1. По известным значениям угла раскрыва  и размерам раскрыва и  найдем фокусное расстояние зеркала:

,                                              (6)

где см – линейный размер раскрыва. Подставив, получим:

 см.

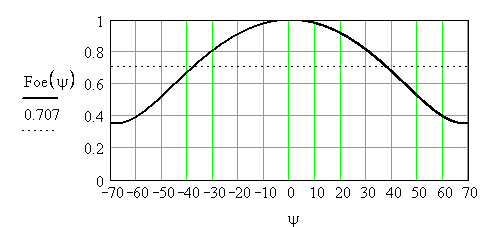
Рис. 3.1 Нормированная ДН облучателя в Е – плоскости

Из графика можно определить ширину ДН облучателя в этой плоскости по половинной мощности: 2^О.

Фокусное расстояние  параболоида вращения (или усеченного параболоида вращения) должно быть одинаково во всех плоскостях. Следовательно, из (6) можем найти угол раскрыва в Н - плоскости: