



Лекция 7.
7. Кинетика реактора
1. Точечная модель динамики реактора: разделение функционала потока на пространственную и временную составляющие.
2. Реактивность реактора,
2.1. Зависимость реактивности от периода реактора
2.2. Запас реактивности
2.3. Реактивность реактора
3. Кинетика с учетом запаздывающих нейтронов
3.1. система дифференциальных уравнений : dn/dt и dC/dt
3.2. решение системы для мгновенных и запаздывающих нейтронов
4. Анализ работы реактора при скачкообразном изменении реактивности
4.1. r=0 (r<<b)
0< r < b
4.2. r < 0
4.3. r > b
7.1. Запаздывающие нейтроны
Запаздывающие нейтроны: источники, времена жизни, 6 групп (табл. 7.1)
Таблица 7.1 - Характеристики групп запаздывающих нейтронов при делении 235U
|
№ группы |
Изотоп-предшественник |
Среднее время жизни предшественника, с |
l предшественника, с-1 |
Доля запаздывающих нейтронов, b ×10-3 |
Средняя энергия запаздывающих нейтронов Е, МэВ |
|
1 |
87Br |
80,0 |
0,0125 |
0,21 |
0,25 |
|
2 |
127I |
33,0 |
0,0303 |
1,41 |
0,56 |
|
3 |
89Br |
9,02 |
0,111 |
1,25 |
0,43 |
|
4 |
135Sb |
3,33 |
0,301 |
2,53 |
0,62 |
|
5 |
85As |
0,89 |
1,135 |
0,73 |
0,42 |
|
6 |
Не известен |
0,332 |
3,01 |
0,26 |
Не известна |
Эффективная доля запаздывающих нейтронов bэфф
Как видно из таблицы 7.1, средняя энергия запаздывающих нейтронов в 4 - 5 раз меньше средней энергии мгновенных нейтронов, следовательно, для замедления до тепловой области запаздывающим нейтронам требуется меньшее число столкновений с ядрами замедлителя - меньше утечка, поэтому доля запаздывающих нейтронов, которые вызовут деление больше, чем b., т.е., их эффективность гораздо выше, чем мгновенных нейтронов (см. таблицу 7.2).
Таблица 7.2 - Параметры запаздывающих нейтронов
|
Период полураспада, с |
Выход нейтронов на деление |
Парциальный выход, b |
|
|
Для деления на тепловых нейтронах |
|||
|
233U |
0.277 - 55.00 |
0.0066 |
0.0026 |
|
235U |
0.230 - 55.72 |
0.158 |
0.065 |
|
239Pu |
0.257 - 54.28 |
0.0061 |
0.0021 |
|
Для деления на быстрых нейтронах |
|||
|
238U |
0.172 - 52.38 |
0.0412 |
0.0148 |
С учетом запаздывающих нейтронов среднее эффективное время жизни (t) одного поколения нейтронов в размножающей среде:
t = (1-b) × tмгн + 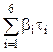 ≈ 0,1 с
≈ 0,1 с
оказывается достаточно большим, что делает возможным управление ЦРД.
Например, если Кэфф =1,005, то Т= t/(кэфф-1) = 0,1/0,005 = 20 с или n/no=exp[(Kэфф-1)/t] = e0,05t, т.е. за 1 с мощность реактора возрастет лишь на 5%. Здесь Т - период реактора - время, за которое количество нейтронов (число делений) возрастает в е раз.
7.2. Кинетика с учетом запаздывающих нейтронов
В промежуток времени t+dt исчезнет n×(dt/tмгн) нейтронов, которые, в сою очередь, создадут Kэфф(1-b)× n×(dt/tмгн) нейтронов другого поколения и Kэффb× n×(dt/tмгн) ядер, дающих запаздывающие нейтроны в количестве åliCi ( здесь li - постоянная распада радиоактивного нуклида - предшественника; ci - концентрация нуклида-излучателя запаздывающих нетронов): dn=[(Кэфф-bКэфф-1)n/tмгн + å liсi]dt
![]() В результате получаем систему уравнений
В результате получаем систему уравнений
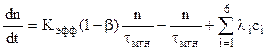
(7.1)
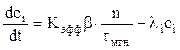
|
Кэфф= |
введем параметр (r - реактивность) r= 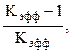 характеризующий степень отклонения
эффективного коэффициента размножения от единицы.
характеризующий степень отклонения
эффективного коэффициента размножения от единицы.
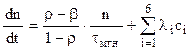
![]() Перепишем ур.-е (7.1) заменив Кэфф на r
Перепишем ур.-е (7.1) заменив Кэфф на r
|
(7.2) |
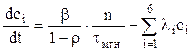
Возьмем среднюю постоянную распада по всем группам запаздывающих нейтронов. Решения этой системы имеют вид eωt. подставив предполагаемое решение в систему (7.2), получим закон изменения плотности нейтронов во времени
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.