n(t) = n(t)мгн +n(t)зап, (7.3)
где
|
(7.4.) |
и
составляющие общего изменения плотности нейтронов за счет собственно мгновенных и запаздывающих нейтронов.
На рисунке 7.1 показано
как изменяются потоки нейтронов при введении положительной (верхняя кривая) и
отрицательной (нижняя кривая) реактивности.
Рис. 7.1. Сравнение переходных процессов при разных знаках r.
Реактивность - величина безразмерная, выражается в долях или процентах. Часто реактивность выражают в долларах 1$ =[r=b], в этом случае одинаковая реактивность в долларах вызывает разгон реактора с одним и тем же периодом независимо от того, на каком делящемся веществе он работает.
7.3. Анализ работы реактора при скачкообразном изменении реактивности
Соотношение экспонент (7.4) в уравнении (7.3) и степень влияния каждой на их общее изменение плотности нейтронов зависят от абсолютной величины и знака возмущения r, вызвавшего переходный процесс.
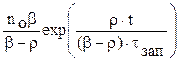
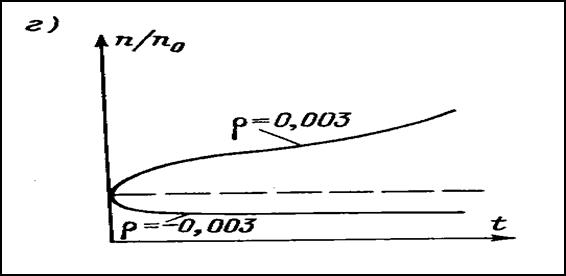
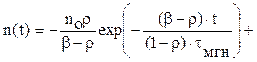(7.5.)
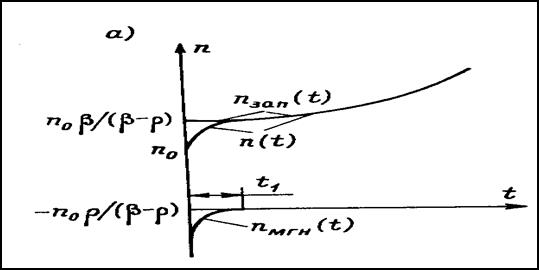
При r=0 (установившийся режим) nмгн = 0, а nзап = no , т.е. реактор критичен на запаздывающих нейтронах, а по отношению к мгновенным реактор подкритичен.
При выводе реактора в накритический режим приложенным к нему положительным возмущением r в зависимости от соотношения r и b возникают два принципиально различных типа переходного процесса.
7.3.1. 0 < r < b
При 0 < r < b, первая экспонента отрицательна, вторая положительна. В момент t=0 сумма экспонент равна no. В начальный момент времени t1 поток нейтронов n(t) быстро возрастает за счет увеличения числа мгновенных нейтронов. Экспонента n(t)мГн, показывающая изменение во времени доли мгновенных нейтронов, быстро стремится к нулю. И по истечении малого времени (~1 с), влияние мгновенных нейтронов на количество нейтронов становится пренебрежимо малым, и дальнейший процесс полностью определяется влиянием запаздывающих нейтронов (рис.7.2 а). По отношению к ним реактор находится в надкритическом состоянии, а плотность нейтронов неограниченно возрастает с периодом измеряющимся десятками секунд
T=(b - r)×tзап/r , (7.6)
При r=0,5b Т=tзап .
Рис. 7.2а Переходные процессы изменения плотности нейтронов в активной зоне при 0 < r < b (кривые построены в соответствии с формулой (7.7.)
Определение периода реактора по (7.6) правомерно только при малых изменениях реактивности, более строгое соотношение между периодом и реактивностью определяется уравнением Нордхейма
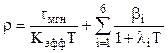(7.7)
7.3.2. r << b
|
Т≈ |
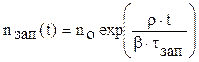
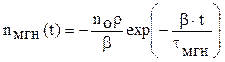При небольших r (<<b) Т практически не зависит от времени жизни нейтронов
7.3.3. r < 0
При скачкообразном отрицательном изменении реактивности (r < 0), обе экспоненты положительны и с течением времени асимптотически стремятся к нулю (рис. 7.2 в) Здесь можно выделить два этапа: быстрое снижение мощности на ú r ê/(b+ú r ê) периодом Т=(1-r)×tмгн/(b+ú rú), обусловленное мгновенными нейтронами. Через доли секунды этот процесс затухает и скорость изменения плотности нейтронов определяется nзап, и поток нейтронов будет уменьшаться с установленным периодом. С увеличением реактивности период будет уменьшаться. Но даже при úrç >> b установившийся период будет приближаться к периоду полураспада наиболее долгоживущей группы запаздывающих нейтронов.
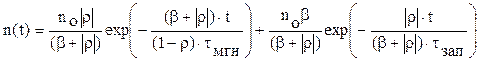(7.8)
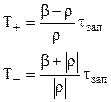Очевидно,
что установившийся период будет разным при введении разнознаковой, но
одинаковой по абсолютной величине реактивности [см Ур. (7.5) и (7.8)], т.е. за
пределами времени действия первой экспоненты изменение потока нейтронов
происходит с разной скоростью.
Установившийся период при введении скачка положительной реактивности
Установившийся период при введении скачка отрицательной реактивности
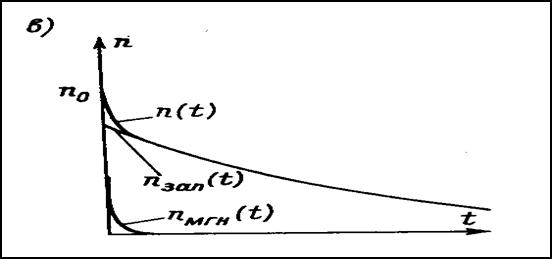Рис. 7.2в Переходные процессы изменения плотности
нейтронов в активной зоне при r < 0 (кривые построены в
соответствии с формулой (7.7.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
