
















МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ СИБСТРИН
Кафедра прикладной математики
Индивидуальное задание
по математической статистике
Выполнила: студентка 253 группы
Соломатина А.А.
Проверил: Соппа М.С.
Новосибирск, 2010г.
СОДЕРЖАНИЕ:
Введение………………………………………………………………………
1 Раздел Точечные оценки неизвестных параметров………………………
Задача…………………………………………………………………
Построить гистограмму……………………………………………
Задача…………………………………………………………………
Задача…………………………………………………………………
Задача…………………………………………………………………
Задача…………………………………………………………………
Раздел 2 Интервальные оценки неизвестных параметров………………
2.1 Задача……………………………………………………………………
2.2 Задача…………………………………………………………………
2.3 Задача…………………………………………………………………
Раздел 3 Проверка статистических гипотез …………………………
3.1.1 Задача………………………………………………………………
3.1.2 Задача……………………………………………………………
3.2.1 Задача…………………………………………………………………
3.2.2 Задача……………………………………………………………
Раздел 4 Оценка ошибки выборки…………………………………………
4.1 Задача……………………………………………………………
Раздел 1. Точечные оценки неизвестных параметров
Математическая статистика — раздел математики, посвященный методам и правилам обработки и анализа статистических данных, т. е. сведений о числе объектов, обладающих определенными признаками, в какой-либо более или менее обширной совокупности. Сами методы и правила строятся безотносительно к тому, какие статистические данные обрабатываются (физические, экономические и др.), но обращение с ними требует обязательного понимания сущности явления, изучаемого с помощью этих правил.
Генеральная совокупность – совокупность результатов всех мыслимых наблюдений, проводимых в кажущихся неизменных условиях над одной из случайных величин X , связанных с данным видом объектов.
Статистический ряд распределения – таблица, в верхней строчке которой записываются все различные элементы выборки, а в нижней строчке – относительные частоты, соответствующие данным элементам.
Обычно в распоряжении имеются лишь данные выборки, например значения количественного признака х1, х2, …, хn, полученные в результате n наблюдений. Через эти данные и выражается оцениваемый параметр. Рассматривая х1, х2, …, хn как независимые случайные величины Х1, Х2, …, Хn, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая и даёт приближённое значение оцениваемого параметра.
Оценкой неизвестного параметра Ѳ называется любая случайная величина Ѳ*, зависящая от (Х1, Х2,…, Хn).
Выборочная средняя хср – это понятие математической статистики — один из основных параметров, характеризующих распределение как выборки, так и генеральной совокупности, это среднее арифметическое значение признака выборочной совокупности.
Выборочная дисперсия Dв – это среднее арифметическое квадратов
отклонения наблюдаемых значений признака от их среднего значения![]() хср.
хср.
Задача 1.1.
Дана выборка Y:
|
3,63 4,52 2,12 3,78 4,62 1,91 4,12 3,85 2,65 2,72 5,79 2,93 4,67 4,72 5,54 3,13 3,16 2,03 2,72 3,49 4,38 4,54 3,42 3,45 2,63 |
4,79 4,70 4,23 5,08 4,17 6,06 4,36 5,52 5,22 6,89 1,42 2,97 5,58 5,70 3,75 6,64 3,62 5,39 3,79 5,67 5,18 3,11 2,42 4,94 5,10 |
Табл.1
Задание: Построить интервальный вариационный ряд, разбив выборку на 5 частей.
Решение: Для построения интервального вариационного ряда необходимо найти максимальное и минимальное значение выборки.
n=50
Ymax=6,64
Ymin=1,42
Находим величину интервала h, используя максимальное и минимальное значение выборки:
h= (Ymax - Ymin)/5,
h= (6,64-1,42)/5=1,044
Теперь строим интервальный вариационный ряд с указанием абсолютных и относительных частот.
Относительная частота – это есть вероятность попадания определённого значения в конкретный интервальный ряд.
|
Y |
F |
ω(Р) |
|
1,42-2,464 |
5 |
0,1 |
|
2,464-3,508 |
12 |
0,24 |
|
3,508-4,552 |
13 |
0,26 |
|
4,552-5,596 |
14 |
0,28 |
|
5,596-6,64 |
6 |
0,12 |
Табл. 2
Границы интервальных рядов считаются по формулам: сi=a + i*h, где i изменяется от 1 до 5.
Задача 1.2.
Построить гистограмму относительных частот, используя интервальный вариационный ряд. Сделать предположение о виде генеральной совокупности.
Решение
Используя данные табл.2, построим гистограмму относительных частот.
Для построения необходимо найти середины интервалов:
1) 1,42 + 0,522 = 1,942
2) 2,464 + 0,522 = 2,986
3) 3,508 + 0,522 = 4,03
4) 4,552 + 0,522 = 5,074
5) 5,596 + 0,522 = 6,118
Гистограмма относительных частот:

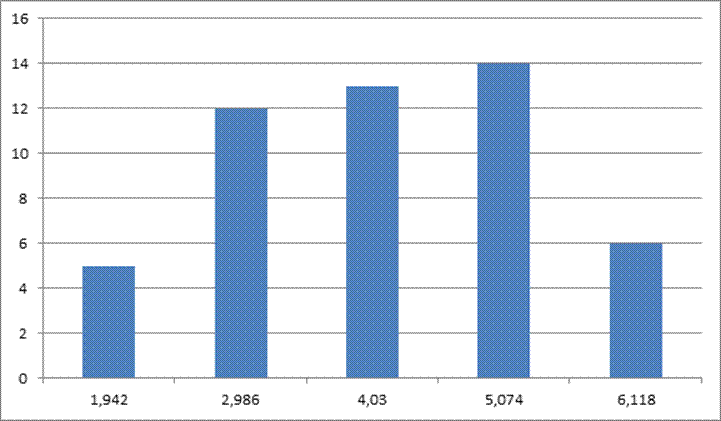
Вывод: По построенной гистограмме мы можем выдвинуть гипотезу о виде распределения генеральной совокупности. Генеральная совокупность распределена по закону близкому к нормальному закону.
Задача 1.3.
Найти двумя способами состоятельную и несмещённую оценку для Хг.
Состоятельной и несмещённой оценкой Хг является Хв.
1-й способ:
Хв = хср. Рассчитаем хср с помощью Excel. В результате этого получим хср=4,1364.
2-й способ
Вычисляем хср приближённо, используя интервальный вариационный ряд.
Для этого находим середины интервалов:
Середины интервалов:
[1,42; 2,464) – 1,942;
[2,464; 3,508) – 2, 986;
[3,508; 4,552) – 4,03;
[4,552; 5,596) – 5,074;
[5,596; 6,64] – 6,118.
Вычисляем по формуле:
хср ≈ а1*ω1 + а2*ω2 +… +аn*ωn,
хср≈1,942*0,1+2,986*0,24+4,03*0,26+5,074*0,28+6,118*0,12≈4,1135
Задача 1.4
Найти двумя способами состоятельную и несмещённую оценку для дисперсий генеральной совокупности.
S2= n/(n-1)*DB.
S2 найти двумя способами.
1-й способ
Найдём значение дисперсии точно, с помощью Excel.
DB= 0,83057.
S2=50/49*0,83057=0,8475.
2-й способ
Найдём значение дисперсии приблизительно по следующей формуле:
DB ≈ а12*ω1 + а22*ω2 +… +аn2*ωn,
S2 ≈50/49*0,913≈0,932.
DB≈(0,1)2*1,942+(0,24)2*2,986+(0,26)2*4,03+(0,28)2*5,074+(0,12)2*6,118 ≈ 0,0192+0,1799+0,2724+0,3978+0,0881 ≈ 0,9574.
S2 ≈50/49*0,9574≈0,9769.
Задача 1.5
Построить корреляционную таблицу
|
Y Х |
[1,42-2,464) |
[2,464-3,508) |
[3,508-4,552) |
[4,552-5,596) |
[5,596-6,64] |
|
[2,18;3,07) |
0,04 |
0,02 |
0 |
0 |
0,02 |
|
[3,07;3,96) |
0,04 |
0,08 |
0,1 |
0,1 |
0,06 |
|
[3,96;4,85) |
0 |
0,08 |
0,08 |
0,12 |
0,02 |
|
[4,85;5,74) |
0,02 |
0,02 |
0,08 |
0,06 |
0,02 |
|
[5,74;6,63] |
0 |
0,04 |
0 |
0 |
0 |
Задача 1.6
Оценить коэффициент корреляции двумя способами: Excel и с помощью корреляционной таблицы. Выдвинуть гипотезу о существовании корреляционной связи между Х и Y.
1 способ
Рассчитываем коэффициент корреляции в Excel: rв =0,2306.
2 способ
Рассчитываем коэффициент корреляции, пользуясь корреляционной таблицей, по следующей формуле:
![]() rв
≈(
x*y
– xср*yср
)/
rв
≈(
x*y
– xср*yср
)/![]() *
*![]() ,
,
![]() x*y=∑∑xiyiωi,,
x*y=∑∑xiyiωi,,
![]() x*y=2,625*(1,942*0,04 +
2,986*0,02 +6,118*0,02) +
x*y=2,625*(1,942*0,04 +
2,986*0,02 +6,118*0,02) +
3,515*(1,942*0,04 + 2,986*0,08 +4,03*0,01+5,074*0,01+6,118*0,06) +
4,405*(2,986*0,08 +4,03*0,08 + 5,074*0,12 + 6,118*0,02) +
5,295*(1,942*0,02 + 2,986*0,02 + 4,03*0,08 + 5,074*0,06 + 6,118*0,02) +
6,185*2,986*0,04 ≈ 17,489
xср =4,223, DX= 0,373.
yср = 4,113, DY=0,977.
rв = (17,489– 4,223*4,113) / (0,611*0,988)= 0,12/0,6037 ≈0,19.
Коэффициент корреляции был посчитан двумя способами и получился примерно одинаковым: rв≈0,19.
На основании полученных данных можно сказать, что между
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.