Аналоговые и дискретные фильтры

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

ЮЖНОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА В г. ТАГАНРОГЕ

Лабораторная работа №3

по курсу ЦОСиСП

«Аналоговые и дискретные фильтры»

Выполнили: cт.гр.Р-74

Егоркин. Е.Г.

Саврасов И.М.

Захарченко И.В.

Проверил:

Крылов А. А.

Таганрог 2007

Цель работы: приобретение навыков расчета и исследования фильтра при помощи MATLAB.

Техническое задание: моделировать процесс фильтрации сигнала с помощью пакета MATLAB с использованием  режекторного фильтра(Батерворда типа 2) со следующими характеристиками:

полоса подавления	250-300 Гц,
полоса пропускания	0-50 кГц, 450-500 кГц
неравномерность в полосе пропускания	3 дБ,
затухание в полосе подавления	20 дБ,
частота дискретизации	1МГц.

Расчет фильтра и построение его АЧХ и ФЧХ

Для нахождения АЧХ и ФЧХ дискретных фильтров используется функция freqz, которая очень похожа на функцию freqs для аналоговых цепей. По умолчанию выбираются 512 частотных точек, равномерно распределенных в диапазоне от 0 до π. Рассчитаем АЧХ и ФЧХ дискретного фильтра:

w1=250000*2*pi

w2=300000*2*pi

Fs=1000000

w1=250000*2/Fs

w2=300000*2/Fs

[b,a]=butter(2,[w1 w2],'stop')

f=0:0.01:pi

h=freqz(b,a,f)

x=f/pi*Fs/2

y=angle(h)*180/pi

y=unwrap(y)

subplot(2, 1, 1)

plot(x,abs(h))

grid on

Получим следующие ЧХ:

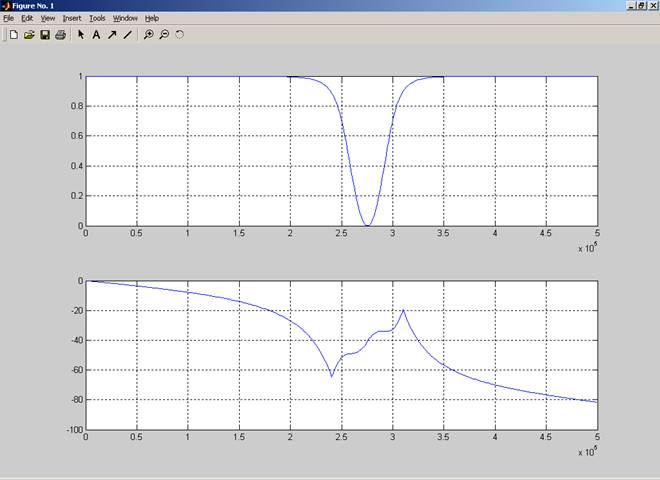
Исследование функции дискретной фильтрации

Основная функция дискретной фильтрации в пакете MATLAB носит имя filter. Она имеет следующий синтаксис:

z=filter(b,a,y);

где z – вектор результирующей фильтрации,

b, a – коэффициенты функции передачи фильтра,

y – вектор значений входного сигнала.

Возьмем фильтр, рассчитанный в предыдущем пункте работы, и пропустим через него сигнал из 2-х гармоник с частотами 50 кГц и 275 кГц (частота дискретизации 1МГц):

Fs=1000000

w1=250000*2/Fs

w2=300000*2/Fs

[b,a]=butter(2,[w1 w2],'stop')

t=0:1/Fs:0.0001

y=sin(2*pi*50000*t)+sin(2*pi*275000*t)

z=filter(b,a,y)

subplot(2,1,1)

plot(t,y)

subplot(2,1,2)

plot(t,z)

Тогда сигнал до и после фильтрации будет иметь вид:

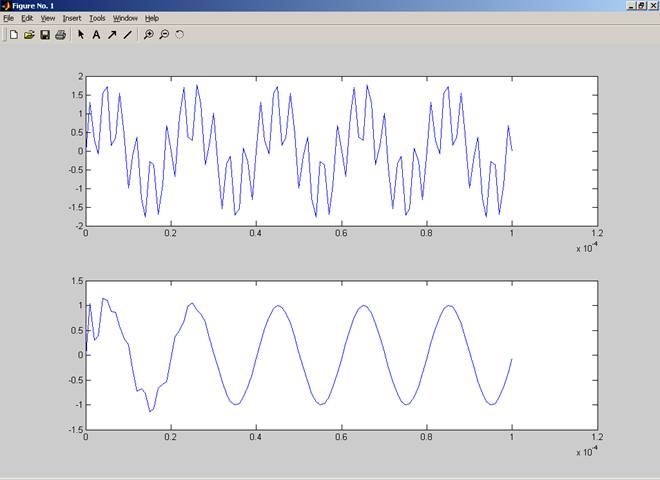
Выводы

В процессе выполнения работы был синтезирован режекторный фильтр Баттерворта 2R  минимального порядка, соответствующий требованиям ТЗ. В качестве входного сигнала была использована аддитивная смесь 2-х гармоник с частотами f₁=25 кГц и f₂=275кГц для того, чтобы проверить избирательные свойства синтезированного фильтра.