аналогии составим уравнения для остальных 3-х интенсивностей и получим систему уравнений Колмогорова для заданной экономической системы.
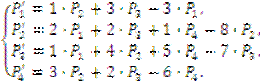
Для решения данной системы необходимо добавить уравнение
![]() .
.
Так как в предельном состоянии системы вероятности являются постоянными величинами, то их производные равны нулю. Поэтому для нахождения предельных вероятностей необходимо решить систему.
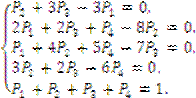
Решив полученную систему, получим:
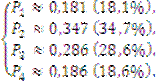
Получили, что в предельном состоянии заданная
экономическая система будет находиться в состоянии ![]() с
вероятностью 0,181, в состоянии
с
вероятностью 0,181, в состоянии ![]() с вероятностью
0,347, в состоянии
с вероятностью
0,347, в состоянии ![]() с
вероятностью 0,286, в состоянии
с
вероятностью 0,286, в состоянии ![]() с
вероятностью 0,186.
с
вероятностью 0,186.
5.8 Процесс гибели и размножения.
Размеченный граф состояний в установившемся режиме для процесса гибели и размножения приведен на рисунке.

Рис. 5.8.1 – Граф состояний процесса гибели и размножения.
Найдите вероятности состояний.
Решение.
Изобразим граф состояний процесса гибели и размножения в общем виде:

Рис. 5.8.2 – Граф общего вида для процесса гибели и размножения.
Для нахождения вероятностей состояний процесса гибели и размножения необходимо воспользоваться формулами:
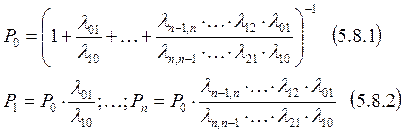
![]()

![]()

Применим данные формулы для вычисления вероятностей состояний заданного процесса.
Найдем вероятность состояния ![]() .
.
![]()
Найдем финальные вероятности остальных состояний системы.
![]()
![]()
![]()
![]()
![]()
Получили, что в состоянии ![]() система
будет находиться 8,45% времени, в состоянии
система
будет находиться 8,45% времени, в состоянии ![]() 25,35%, в
состоянии
25,35%, в
состоянии ![]() 12,68%, в
состоянии
12,68%, в
состоянии ![]() 8,45%, в
состоянии
8,45%, в
состоянии ![]() 16,9%, в
состоянии
16,9%, в
состоянии ![]() 28,17%.
28,17%.
5.9 Одноканальные системы массового обслуживания с отказами.
Автозаправочная станция (АЗС) имеет одну заправочную колонку. Площадка при станции не допускает пребывание машин в очереди на заправку. Поток машин, прибывающих для заправки, имеет интенсивность 1 машина в минуту. Процесс заправки продолжается в среднем 1,25 мин. Определить: вероятность отказа; относительную и абсолютную пропускную способности АЗС.
Решение.
По условию АЗС имеет 2 заправку, значит, она является 1-канальной СМО. Так как площадка на станции не допускает пребывание машин в очереди, то если машина обслуживается, другие получат в это время отказ, значит, данная СМО является 1-канальной СМО с отказами.
![]()
Данная СМО имеет 2 состояния: ![]() – канал
свободен,
– канал
свободен, ![]() – канал
занят.
– канал
занят.
Этим состояниям соответствуют вероятности ![]() и
и ![]() .
.
Запишем формулы для их вычисления:
![]()
![]()
Необходимо найти вероятность отказа в обслуживании. В
данном случае, если канал занят, т.е. система находится в состоянии ![]() , то заявка
получает отказ, следовательно, вероятность отказа равна вероятности нахождения
системы в состоянии
, то заявка
получает отказ, следовательно, вероятность отказа равна вероятности нахождения
системы в состоянии ![]() , т.е.
, т.е.
![]()
![]() – относительная
пропускная способность системы, т.е. часть автомобилей, обслуживаемых системой,
из всех автомобилей, которые приезжают на АЗС.
– относительная
пропускная способность системы, т.е. часть автомобилей, обслуживаемых системой,
из всех автомобилей, которые приезжают на АЗС.
В данном случае относительная пропускная способность равна вероятности того, что АЗС свободна.
![]()
Чтобы найти абсолютную пропускную способность системы, необходимо воспользоваться следующей формулой:
![]()
Найдем необходимые показатели эффективности по формулам (5.9.3) – (5.9.5).
![]()
![]()
![]()
![]()
Итак, получили, что из всех приезжавших на АЗС автомобилей, обслуживается в среднем только 44%, остальные 56% получают отказ в обслуживании.
В среднем за минуту обслуживается 0,44 автомобиля.
Полученные характеристики АЗС указывают на то, что СМО работает неэффективно, поэтому необходимо увеличивать количество заправочных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.