Определение показателей и характеристик надежности информационной системы, страница 4

Решение:

Основная не резервированная система состоит из N = 16 блоков со средним временем наработки на отказ одного блока  (ч).

Кратность общего резервирования с постоянно включенным резервом равна M = 7.

1.  Определим интенсивность отказа одного элемента основной системы по формуле (2.1)

                                     (2.1)

2.  Определим интенсивность отказа основной системы или любой из резервных систем по формуле (2.2)

                                        (2.2)

 (1/ч).

3.  Определим среднее время наработки на отказ резервированной системы по формуле (2.3)

                                 (2.3)

4.  Определим интенсивность отказов резервированной системы по формуле 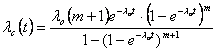(2.4)

                           (2.4)

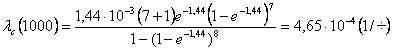
5.  Определим вероятность безотказной работы резервированной системы по формуле (2.5)

                         (2.5)

6.  Построим график зависимости вероятности безотказной работы от времени работы системы.

Данные, рассчитанные по формуле (2.5) приведены в табл. 2.2, а график зависимости показан на рис. 2.1.

 Таблица 2.2        

T	Р(t)
0	1
200	0,999984624
400	0,998648976
600	0,987451547
800	0,95208981
1000	0,885045693
1200	0,790830363
1400	0,681284833
1600	0,568991477

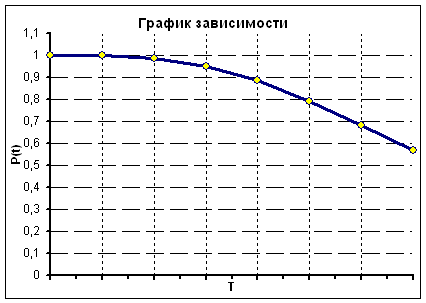                                                                                    Рис. 2.1

Задача №3

Определить показатели надежности информационной системы, построенной по N-ированной мажоритарной схеме, с интенсивностью отказов основной системы λ. Время работы системы t =1000ч. Вариант задания определяется по двум последний цифрам шифра в соответствии с табл. 3.1. По последней цифре шифра определяется тип мажоритарной системы, по предпоследней - интенсивность отказов.

Таблица 3.1