












Установить соответствие между понятиями.
|
Типы моделей |
Характеристики моделей |
|
Детерминированные |
Результаты на выходе модели однозначно определяются управляющими воздействиями |
|
Стохастические |
При задании на входе определенной совокупности значений на выходе модели могут получиться различные результаты в зависимости от действия случайных факторов |
|
Статические |
Все зависимости отнесены к одному моменту или периоду времени, без учета изменения их параметров |
|
Динамические |
Описывают экономические системы в развитии, отражают зависимость переменных от времени и их взаимосвязь во времени |
|
Микроэкономические |
Описывают взаимодействия структурных и функциональных составляющих экономики, связаны с предприятиями и фирмами |
|
Макроэкономические |
Отражают функционирование экономики как единого целого, связывают между собой укрупненные материальные и финансовые показетели |
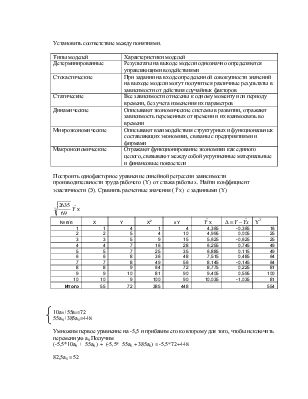
Построить однофакторное уравнение линейной регрессии
зависимости производительности труда рабочего (Y) от
стажа работы x. Найти коэффициент эластичности (Э).
Сравнить расчетные значения (![]() х) с заданными (Y)
х) с заданными (Y)
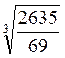
![]() х
х
|
№ п/п |
Х |
Y |
X2 |
xY |
|
|
Y2 |
|
1 |
1 |
4 |
1 |
4 |
4,365 |
-0,365 |
16 |
|
2 |
2 |
5 |
4 |
10 |
4,995 |
0,005 |
25 |
|
3 |
3 |
5 |
9 |
15 |
5,625 |
-0,625 |
25 |
|
4 |
4 |
7 |
16 |
28 |
6,255 |
0,745 |
49 |
|
5 |
5 |
7 |
25 |
35 |
6,885 |
0,115 |
49 |
|
6 |
6 |
8 |
36 |
48 |
7,515 |
0,485 |
64 |
|
7 |
7 |
8 |
49 |
56 |
8,145 |
-0,145 |
64 |
|
8 |
8 |
9 |
64 |
72 |
8,775 |
0,225 |
81 |
|
9 |
9 |
10 |
81 |
90 |
9,405 |
0,595 |
100 |
|
10 |
10 |
9 |
100 |
90 |
10,035 |
-1,035 |
81 |
|
Итого |
55 |
72 |
385 |
448 |
554 |
![]()
10а0+55а1=72
55а0+385а1=448
Умножим первое уравнение на -5,5 и прибавим его ко второму для того, чтобы исключить переменную а0. Получим
(-5,5*10а0 + 55а0 ) + (-5,5* 55а1 + 385а1) = -5,5*72+448
82,5а1 = 52
а1 =0,63
Подставим полученное значение а1 в первое уравнение
10а0+55*0,63=72
а0= 3,735
Вычислим ![]() х для всех хi
х для всех хi
Коэффициент регрессии а1 показывает, что при увеличении стажа работы на год, дневная выручка рабочего увеличивается на 0.63 шт. в день.
Вычислим коэффициент эластичности
Эх=а1![]()
![]() =
= ![]() =5,5;
=5,5;
![]() =
= ![]() =7,2;
Эх=0,63
=7,2;
Эх=0,63![]() =0,48
=0,48
Коэффициент эластичности показывает, что дневная выработка изменится на 0.48% при увеличении стажа на 1%.
![]()
Рассчитаем коэффициент парной корреляции
2 2


![]() хi = 55;
хi = 55; ![]() Yi = 72;
Yi = 72; ![]() хiYi
= 448;
хiYi
= 448; ![]() хi
= 3025;
хi
= 3025; ![]() Yi = 5184;
Yi = 5184; ![]() х
х![]() = 385;
= 385; ![]() Y
Y![]() = 554;
= 554;
r= 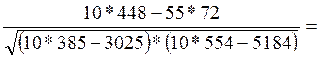 0,4465
0,4465
Между квалификацией работника и дневной выработкой существует прямая, слабая корреляционная связь.
Установить соответствие между понятиями
|
Значение линейного коэффициента корреляции |
Характер связи |
|
r=0 |
Отсутствует |
|
r=1 |
Функциональная |
|
r≤| ±0.3| |
Практически отсутствует |
|
|±0,3|≤r≤|±0,5| |
Слабая |
|
|±0,5|≤r≤|±0,7| |
Умеренная |
|
|±0,7|≤r<|±1,0| |
Сильная |

|
1 |
|
σx= |
|
2 |
|
σy= |
|
3 |
|
r= |
|
4 |
|
а1=0,57· |
|
5 |
|
Y=4+08x |

|
1 |
|
σx= |
|
2 |
|
σy= |
|
3 |
|
r= |
|
4 |
|
а1=0,88· |
|
5 |
|
Y=5.2+1.76x |

|
1 |
|
Y=2,3 + (-1,2x)=2,3-,1,2x |
|
2 |
|
Э= -1,2· |

|
1 |
|
Y=4,9 +0,2x |
|
2 |
|
Э= 0,2· |

|
1 |
|
У0 =У1996=21,2 |
|
2 |
|
У1 = У1997 =22,4 |
|
У2 = У1998 =24,9 |
||
|
У3 = У1999 =28,6 |
||
|
У4 = У2000 =31,6 |
||
|
3 |
|
∆ |
|
∆ |
||
|
∆ |
||
|
∆ |
||
|
4 |
|
∆ |
|
∆ |
||
|
∆ |
||
|
∆ |

|
1 |
|
У0 =У1996=95,2 |
|
2 |
|
У1 = У1997 =100 |
|
У2 = У1998 =104 |
||
|
У3 = У1999 =110 |
||
|
У4 = У2000 =115 |
||
|
3 |
|
∆ |
|
∆ |
||
|
∆ |
||
|
∆ |
||
|
4 |
|
∆ |
|
∆ |
||
|
∆ |
||
|
∆ |

|
1 |
|
У0 =У1996=21,2 |
|
2 |
|
У1 = У1997 =22,4 |
|
У2 = У1998 =24,9 |
||
|
У3 = У1999 =28,6 |
||
|
У4 = У2000 =31,6 |
||
|
|
||
|
3 |
|
К |
|
К |
||
|
К |
||
|
К |
||
|
4 |
|
Т |
|
Т |
||
|
Т |
||
|
Т |
||
|
5 |
|
К |
|
К |
||
|
К |
||
|
К |
||
|
6 |
|
Т |
|
Т |
||
|
Т |
||
|
Т |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.