5. Даем единичное приращение по координате X5=7+1=8 и производим суммирование значения R=R+(Yк-Yн)=3+5=8 и сравниваем c (Xк-Xн)=11. Так как условие (2.34) не выполняется, то ∆Y5=0. Отмечаем точку с координатами X5=8; Y5=4 (R=8).
6. Даем приращение по координате X: X6=6+1=9, производим суммирование предыдущего результата R=8 со значением (Yк-Yн)=5, получаем в результате 13, условие (2.34) выполняется. Следовательно, ∆Y6=1. Отмечаем точку с координатами X6=9; Y6=5. Вычитаем из полученной суммы 11, получаем остаток R=2.
7. Даем единичное приращение по координате X7=9+1=10 и производим суммирование значения R=R+(Yк-Yн)=2+5=7 и сравниваем c (Xк-Xн)=11. Так как условие (2.34) не выполняется, то ∆Y7=0. Отмечаем точку с координатами X7=10; Y7=5 (R=7).
8. Даем приращение по координате X: X8=10+1=11, производим суммирование предыдущего результата R=7 со значением (Yк-Yн)=5, получаем в результате 12, условие (2.34) выполняется. Следовательно, ∆Y8=1. Отмечаем точку с координатами X8=11; Y8=6. Вычитаем из полученной суммы 11, получаем остаток R=1.
9. Даем единичное приращение по координате X9=11+1=12 и производим суммирование значения R=R+(Yк-Yн)=1+5=6 и сравниваем c (Xк-Xн)=11. Так как условие (2.34) не выполняется, то ∆Y9=0. Отмечаем точку с координатами X9=12; Y9=6 (R=6).
10. Даем приращение по координате X: X10=12+1=13, производим суммирование предыдущего результата R=6 со значением (Yк-Yн)=5, получаем в результате 11, условие (2.34) выполняется. Следовательно, ∆Y10=1. Отмечаем точку с координатами X10=13; Y10=7. Вычитаем из полученной суммы 11, получаем остаток R=0.
11. Даем единичное приращение по координате X11=13+1=14 и производим суммирование значения R=R+(Yк-Yн)=0+5=5 и сравниваем c (Xк-Xн)=11. Так как условие (2.34) не выполняется, то ∆Y1=0. Отмечаем точку с координатами X11=14; Y11=7 (R=5).
12. Xк=X11=14 и Yк=Y11=7 Алгоритм выполнен полностью полученная аппросксимация показана на рис. 1 из которого видно что отклонение
аппроксимирующих точек от прямой не превышает половины единицы
дискретности.
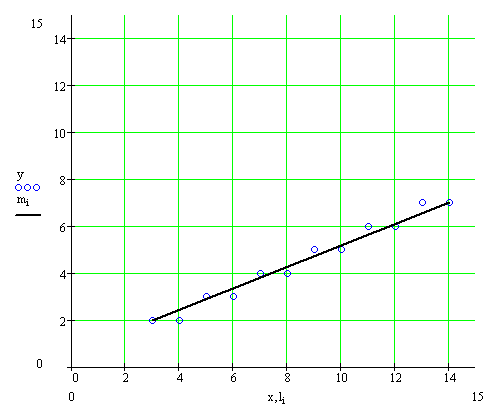
Рис. 1
График аппроксимации отрезка прямой точечными ЭО
(элементами отображения)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.