





















2. Термодинамические процессы
2.1. Теплоёмкость
2.1.1.Вычислить удельные теплоемкости ср и сV гелия He, водорода H2 и углекислого газа СO2.
Решение
1. Удельные теплоёмкости газов определяются их молярной массой и числом степеней свободы молекул
![]() ,
, ![]() .
(1)
.
(1)
2. Молярные массы заданных газов: m(He) = 4×10 3 кг/моль; m(H2) = 2×10 3 кг/моль; m(CO2) = 44×10 3 кг/моль; i(He) = 3; i(H2) = 5; i(CO2) = 6.
3. Вычислим удельные теплоёмкости
гелия: ![]() ,
, ![]() , (2)
, (2)
водорода: ![]() ,
, ![]() , (3)
, (3)
углекислого газа: ![]() ,
, ![]() .
(4)
.
(4)
2.1.2. Разность удельных теплоёмкостей некоторого газа cp cV равна 260 Дж/кг×К. Определить молярную массу этого газа.
Решение
1. Запишем уравнение разности удельных теплоёмкостей
![]() , (1)
, (1)
и разрешим полученное уравнение относительно молярной массы m
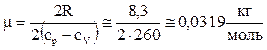 . (2)
. (2)
Очевидно, что заданным газом является молекулярный кислород О2, представляющий собой двухатомную молекулу с числом степеней свободы i = 5.
2.1.3. Определить удельную теплоемкость сV смеси, состоящей из m1 = 10 граммов кислорода О2 и m2 = 20 граммов азота N2.
Решение
1. Для нагревания смеси газов на DТ требуется количество тепла DQ, определяемое уравнением
![]() , (1)
, (1)
где сV теплоемкость смеси.
2. С другой стороны, количество тепла, расходуемое на нагревании смеси может быть представлено так
![]() , (2)
, (2)
3. Приравняем правые части уравнений (1) и (2)
![]()
![]() ,
(3)
,
(3)
где сV1 удельная теплоёмкость кислорода, сV2 удельная теплоёмкость азота.
4. Подставим в уравнение (3) значения удельных теплоёмкостей газов
![]()
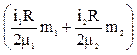 , (4)
, (4)
где i1 = i2 = 5 число степеней свободы молекул газа, m1 = 32×10 3 кг/моль,
m2 = 28×10 3 кг/моль молярные массы газов.
5. Разрешим уравнение (4) относительно cV
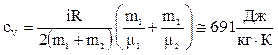 . (5)
. (5)
2.1.4. Определить удельную теплоемкость ср смеси, состоящей из m1 = 10 граммов кислорода О2 и m2 = 20 граммов азота N2.
Решение
1. Воспользуемся уравнением (3) предыдущей задачи и перепишем его следующим образом
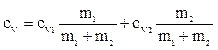 , (1)
, (1)
где v1 = m1/(m1 + m2) массовая доля кислорода, v2 = m2/(m1 + m2) массовая доля азота.
2. Удельная теплоёмкость смеси ср можно представить по аналогии с уравнением (1) так
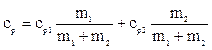 ,
(2)
,
(2)
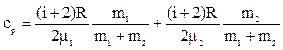 ,
(3)
,
(3)
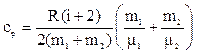 .
(4)
.
(4)
3. Подставим в уравнение (4) значения характеристик газов: i = 5; m1 = 32×10 3 кг/моль; m2 = 28×10 3 кг/моль
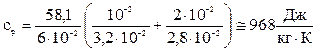 . (5)
. (5)
2.1.5. Определить удельную теплоёмкость сV смеси газов, содержащей V1 = 5 л атомарного водорода, и V2 = 3 л гелия, если газы находятся в одинаковых условиях.
Решение
1.Выразим массы газов из уравнения Клапейрона Менделеева
![]() . (1)
. (1)
2. Подставим далее, полученные значения масс в уравнение (1) задачи 2.1.4
![]() . (2)
. (2)
3. Подставим в уравнение (2) значения удельных теплоемкостей газов сV1 и cV2
![]() ,
,
![]() ,
,
![]() , (3)
, (3)
4. Подставим значения величин, входящих в последнее уравнение
![]() . (4)
. (4)
2.1.6. Определить удельную теплоёмкость ср смеси кислорода и азота, если количество вещества первого компонента равно n1 = 2 моль, а второго компонента n1 = 4 моль.
Решение
1. Выразим массы газов
![]() . (1)
. (1)
2. Подставим значения масс в уравнение (4) задачи 2.1.4
![]() . (2)
. (2)
3. Молярные массы газов равны: m1 = 32×10 3 кг/моль; m2 = 28×10 3 кг/моль. Кислород и азот состоят из двухатомных молекул, поэтому число степеней свободы равно i = 5
![]() . (3)
. (3)
2.1.7. Определить удельную теплоёмкость сV смеси азота и аргона, находящихся в одном баллоне, если массовые доли этих газов v1 и v2 одинаковы и равны v = 0,5
Решение
1. Запишем уравнение (1) задачи 2.1.4 в следующем виде
![]() . (1)
. (1)
2. Молекула азота состоит из двух атомов, поэтому: m1 = 28×10 3 кг/моль, i1 = 5, молекула аргона одновалентна m2 = 40×10 3 кг/моль, i2 = 3
 . (2)
. (2)
2.1.8. Хлор и криптон в атомарном состоянии, взятые в равных объемах, находятся в одинаковых условиях. Определить удельную теплоемкость ср смеси.
Решение
1. Для определения удельной теплоемкости воспользуемся уравнением (1) задачи 2.1.4
![]()
![]() ,
,
2. Хлор и криптон имеют следующие параметры: m1 = 35×10 3 кг/моль, m2 = 84×10 3 кг/моль, i1 = i2 = 3, переписать последнее уравнение следующим образом
![]() . (1)
. (1)
2.1.9. Определить удельную теплоемкость сV смеси ксенона и кислорода, если количества вещества газов одинаковы и равны n.
Решение
1. Выразим массы газов через количества вещества
![]() . (1)
. (1)
2. Запишем уравнение удельной теплоемкости смеси газов
![]() , (2)
, (2)
и проведем очевидные преобразования
![]() , (3)
, (3)
![]() ,
(4)
,
(4)
где i1 = 3 число степеней свободы молекул ксенона, m1 = 0,131×кг/моль молярная масса ксенона, i2 = 5 число степеней свободы двухатомной молекулы кислорода, m2 = 32×10 3 кг/моль молярная масса кислорода.
3. Подставим параметры газов в уравнение (4)
![]() . (5)
. (5)
2.1.10. Степень диссоциации газообразного водорода a = 0,6. Определить удельную теплоемкость cV такого частично диссоциированного газа.
1. Решение
1. Процесс диссоциации заключается в том, что двухатомные молекулы под действием внешних условий электрического, механического, физического или термодинамического характера, распадаются на отдельные атомы.
2. Предположим далее, что в исходном состоянии в рассматриваемом объеме содержалось N двухатомных молекул водорода. После диссоциации будет иметь место смесь двух газов: молекулярного и атомарного водорода, причем 40% от общего количества будут составлять двухатомные молекулы, а 60% одноатомные. Пусть масса одного атома водорода равна m0, в этом случае массы этих газов, составляющих смесь, можно представить следующим образом
![]() ,
(1)
,
(1)
где М первоначальная масса недиссоциированного водорода
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.