Вопрос 82. Биномиальная модель оценки стоимости опционов.
Квалифицированным участникам рынка опционной торговли требуются модели, позволяющие дать точную оценку опционов. Одной из таких моделей является биномиальная модель ценообразования, известная также как модель Кокса–Росса–Рубинштейна.
Биномиальная модель опционного
ценообразования предполагает, что фактические события, связанные с изменением
курсов базисных акций, происходят не случайном образом, а регулярно, с
определенным шагом во времени, или, другими словами, дискретно. Кроме того,
предполагается, что каждое изменение курса акций может осуществляться в двух
режимах: он (курс) может подняться по определенной процентной ставке или по
определенной процентной ставке понизиться.Процентные ставки, определяющие
величину изменений курса акций, устанавливаются таким образом, чтобы покрыть
всю ширину «типического» отклонения цены акций вверх и вниз. В частности, для
курса, повышающегося в конкретном дискрете (периоде) времени, процентную ставку
устанавливают в диапазоне ![]() ; для падающего курса –
в диапазоне
; для падающего курса –
в диапазоне ![]() , где
, где ![]() –
средняя арифметическая попериодных относительных изменений («процентов») курса
акций, а s – стандартное (среднеквадратическое отклонение).
–
средняя арифметическая попериодных относительных изменений («процентов») курса
акций, а s – стандартное (среднеквадратическое отклонение).
На рис. 1 представлена биномиальная ветвящаяся структура, соответствующая описанным выше условиям применения рассматриваемой модели опционного ценообразования.
На рис. 1 S0 – это цена базисной акции на момент оценки стоимости опциона. Каждое увеличение цены акции пропорционально некоторому параметру u и происходит с вероятностью р, каждое уменьшение цены акции пропорционально параметру d и реализуется с вероятностью (1 – р). Например, после первого шага цена акции может быть uS0 или dS0. Если u и d различны по величине, распределение цены акции относительно S0 будет несимметричным.
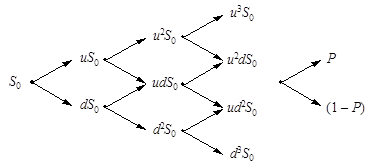 Рис. 1. Биномиальная модель опционного ценообразования
Рис. 1. Биномиальная модель опционного ценообразования
В биномиальном процессе со многими периодами оценка опциона осуществляется начиная с заключительного временного периода двигаясь назад к текущему моменту (на рис. 1 справа налево).
Математические особенности биномиального процесса обеспечивают вполне приемлемую для трейдеров скорость расчетов по модели. Так, из рис. 1 видно, что одношаговое повышение цены, за которым следует одношаговое ее понижение, приводит к тому же результату, что и одношаговое понижение цены, за которым следует одношаговое повышение. Это уменьшает количество всех возможных вариантов цен и сокращает время расчетов.
Большинство компьютерных программ, реализующих биномиальную модель опционного ценообразования, позволяют пользователю самостоятельно задавать число шагов, необходимых для оценивания опционов с требуемой точностью. Обычно, если срок «жизни» опциона невелик, ограничиваются не более, чем 50 шагами.
Центральным моментом расчета стоимости опциона в биномиальной модели является использования идеи дублируещего (репликативного) инвестиционного портфеля, основанного на предложении, что на развитом и эффективном рынке любые два финансовых инструмента (или портфеля инструментов), полностью эквивалентные друг другу по уровню полезности, должны иметь одинаковую привлекательность (ценность) для инвестора.
Учитывая это, всегда можно подобрать дублирующий портфель из рыночных ценных бумаг, который дает такую же отдачу, как и конкретный опцион, а следовательно, имеет такую же рыночную стоимость. Эту концепцию иногда называют условием нулевого арбитража или законом единой цены – на основании того факта, что активы, обеспечивающие одинаковую отдачу, должны также иметь одинаковую цену в отсутствие арбитражных прибылей.
Так, покупку опциона колл на какую-либо акцию можно заменить (продублировать) эквивалентным инвестиционным портфелем – приобретением некоторого количества этих акций на заемные деньги.
Действительно, когда вы покупаете опцион колл, то получаете право через некоторое время (заплатив за акции деньги) получить эти акции в собственность.
Когда вы покупаете акции на заемные деньги, вы также получаете право через определенное время (выплатив долг) получить эти акции в собственность. Таким образом, эквивалентность рассматриваемого опциона и дублирующего инвестиционного портфеля здесь очевидна.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.