Другие предметы \ Радиопередающие устройства

Проектирование схемы передатчика производственной связи с определёнными электрическими параметрами. Полная принципиальная схема рассчитанных каскадов передатчика с элементами цепей питания, страница 7

2.  По предложенным формулам находим следующие параметры:

Амплитуда колебаний напряжения коллектор-эмиттер:

Амплитуда первой гармоники коллекторного тока:

Мощность, отдаваемая цепью коллектора:

Сопротивление и проводимость коллекторной нагрузки:

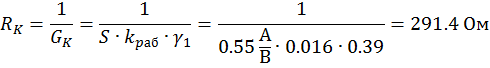
Проводимость коллекторной нагрузки:

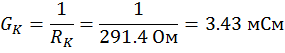
Электрический расчёт параметров контура автогенератора.

Для обеспечения требуемой стабильности частоты необходимо выбирать контур с высокой добротностью, предел изменения которой   (добротность ненагруженного контура) и большим характеристическим сопротивлением , что и определяет резонансное сопротивление контура при полном

включении  , т.к. необходимо обеспечить колебания с высокой стабильностью частоты и малой мощностью в нагрузке, то параметры контура выбираются так, чтобы добротность нагруженного контура  была наибольшей.

Задаёмся необходимым значением добротности:

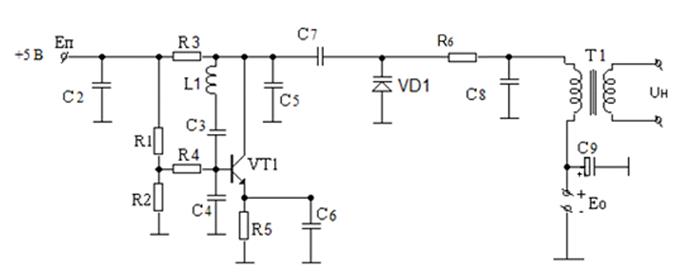
Для расчёта выберем принципиальную схему автогенератора с ёмкостной трёхточкой, которая обеспечивает лучшую стабильность частоты за счёт зависимости от добротности контура и постоянства его параметров.

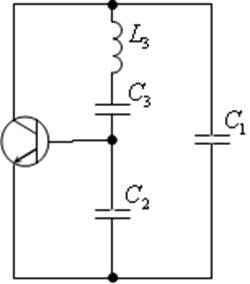
Рис 3. Принципиальная схема автогенератора с дополнительной ёмкостью C3

(схема Клаппа).

Характеристическое сопротивление контура находим по формуле:

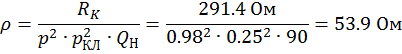
коэффициент включения Клаппа, примем  

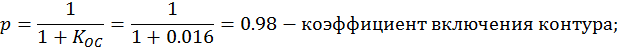
Рассчитывает ёмкость коллекторной нагрузки:

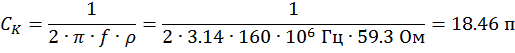
Определяем ёмкости в схеме автогенератора:

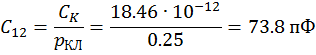
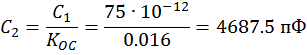
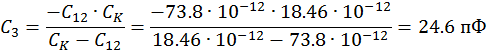
Индуктивность контура:

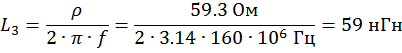
     В техническом задании требуется реализовать автогенератор с высокой стабильностью. Для этой цели можно использовать кварцевые генераторы (Δf/f = 10−6-10−10), который представляет собой автогенератор электромагнитных колебаний с колебательной системой, в состав которой входит кварцевый резонатор. Он предназначен для получения колебаний фиксированной частоты с высокой температурной и временной стабильностью, низким уровнем фазовых шумов.

6.  Электрический расчёт частотного модулятора.

Безымянный.png     По техническому заданию необходимо получить частотную модуляцию сигнала в передатчике. Модуляцию такого типа можно получить путём изменения частоты автогенератора с параметрической стабилизацией. Суть которой состоит в подключении к контуру автогенератора частотный модуляторуправляемый реактивный элемент. В качестве такого используется варикап. Расчёт частотного модулятора проводим в соответствии с учебником [5,стр.376].

Рис 4. Принципиальная схема автогенератора с ЧМ.

В качестве варикапа выбираем КВ 113 А. Минимальное и максимальное значение ёмкости равно , которая меняется при обратном напряжении .

Для передатчика необходимо получить девиацию частоты  при частоте автогенератора . Суммарная ёмкость автогенератора равна . Задаёмся величиной напряжением смещения варикапа  и ёмкостью связи . Ёмкость варикапа при таком смешении равна . Определяем коэффициенты связи:

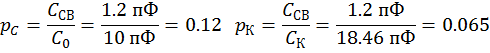
Из формулы определения девиации частоты по первой гармонике модулирующего сигнала находим коэффициент:

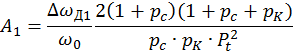
где

;

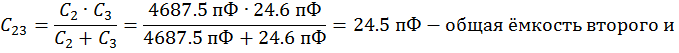
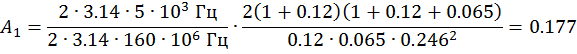
Из таблицы 10-1 учебника [5,стр.377] для коэффициента , находим формулу для вычисления первого коэффициента ряда Маклорена:

Отсюда выражаем коэффициент глубины модуляции:

Решая это уравнение, получаем два результата:

Выбираем .Другое значение физического смысла не имеет. При  увеличении глубины модуляции увеличивается девиация частоты, что приводит к возрастанию коэффициента нелинейных искажений, помимо этого возможно явление паразитной амплитудной модуляции сигнала.

Определим требуемую амплитуду модулирующего сигнала на входе частотного модулятора т.е. амплитуду напряжения приложенную к варикапу:

 При частотной модуляции с помощью варикапа происходит смещение средней частоты называемая отношением девиацией частоты к средней частоте сигнала:

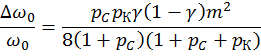
Отсюда требуемое значение девиации частоты:

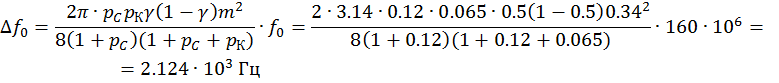
По заданию при проектирование ЧМ необходимо обеспечить девиацию частоты не более  кГц в нашем случае при коэффициенте модуляции  получаем  кГц, что удовлетворяет поставленной цели.

Коэффициент нелинейных искажений через коэффициенты ряда Маклорена:

Скачать файл