Юрий
Волков о возможности превышения скорости света
10 февраля 2003, membrana (staff@membrana.ru)
|
|
Привяжем к столбу лошадь и с помощью динамометра измерим силу, с которой животное может тянуть столб. Особо не напрягаясь, лошадь сможет развить усилие порядка F = 1000 Ньютон.
Привяжем к лошади гирьку массой m = 1г и вычислим, какое ускорение может придать лошадь этой гирьке:
dv/dt= F/m = 103/10-3 = 106 м/с2 (1)
Нетрудно подсчитать, что через 100 секунд ускоренного движения наша лошадь ускорит привязанную к ней гирю до субсветовой скорости.
Абсурдность этого вывода очевидна: лошадь может двигаться со скоростью от силы метров 15 в секунду. Отсюда следует, что максимальная скорость, до которой она может ускорить привязанную к ней гирю (сколь бы не мала была её масса) не превысит этого значения.
Заменим термины: вместо лошади — ускоряющая электромагнитная волна в ускорителе элементарных частиц, а вместо гири — элементарная частица.
Спрашивается, до какой скорости можно ускорить элементарную частицу в этом ускорителе.
По аналогии с лошадью ответ очевиден: до скорости распространения электромагнитной волны в ускоряющем тракте установки, и не более, поскольку именно с этой скоростью подводится энергия от ускорителя к ускоряемой частице.
То есть причину ограничения скорости движения частиц в ускорителе и предельную величину этой скорости можно объяснить без каких-либо манипуляций с массой ускоряемых частиц.
Просвещенная публика может заявить, что аналогия с лошадьми и гирями в таком серьёзном вопросе неуместна. Хорошо. Давайте рассуждать формально.
Частота и соответственно энергия ускоряющей электромагнитной волны в системе отсчёта ускоряемой частицы согласно эффекту Доплера равна:
W = hv0(1-v/u) (2)
где W — энергия ускоряющей электромагнитной волны;
v0 — частота волны в системе неподвижного наблюдателя;
v — скорость движения ускоряемой частицы;
u — скорость распространения волны в тракте ускорителя;
h — постоянная Планка.
Из (2) следует, что при v = u энергия ускоряющей волны в системе отсчёта ускоряемой частицы становится нулевой. То есть, по достижении частицей этой скорости, эффективность ускорителя становится равной нулю.
Отсюда следует, что средствами электромагнитного взаимодействия передать ускоряемой частице неограниченное количество энергии невозможно.
Этому препятствует эффект Доплера. И, во-вторых, предел ускорения определяется не абстрактной скорость света в вакууме с, а вполне конкретной скоростью u, которая определяется качеством изготовления элементов ускорителя.
Скептики могут возразить, что соотношение (2) записано для классического, а не релятивистского эффекта Доплера. Уверяю (а кто не верит, пусть лично проверит), что рассуждения в рамках релятивистского эффекта Доплера приведут к тому же выводу.
Запишем уравнение движения частицы в тракте ускорителя:
d(mv) = qEdt (3)
где m, q — масса и заряд частицы;
Е — напряжённость ускоряющего поля.
В релятивистской механике считается, что Е и q — инварианты относительно v, а масса частицы зависит от этой скорости так:
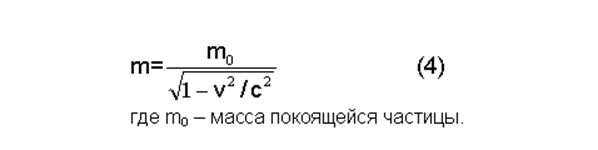
Подставим (4) в (3). После преобразований получим:
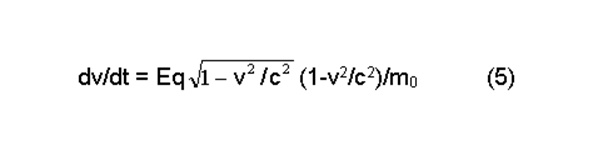
Инвариантность E и q относительно v означает, что сила, ускоряющая частицу, не зависит от скорости этой частицы. Но это заведомо неверная посылка (смотрите выше парадокс с лошадью).
И, тем не менее, уравнение (5) абсолютно точно описывает движения частиц в ускорителе.
Попытаемся разобраться в причинах этого парадокса.
Как известно, чтобы измерить величину электрического заряда, необходимо измерить интенсивность его взаимодействия с другим (пробным) зарядом.
Выше было показано, что интенсивность этого взаимодействия будет зависеть (за счёт эффекта Доплера) от скорости их взаимного движения.
То есть величина электрического заряда будет как-то зависеть от скорости его движения относительно наблюдателя.
Будем считать, что:
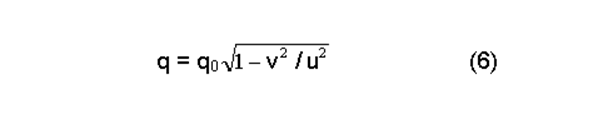
где q — величина электрического заряда, движущегося относительно наблюдателя со скоростью v;
q0 — величина электрического заряда в системе отсчета неподвижного наблюдателя;
u — скорость распространения электромагнитных волн в среде, в которой движется заряд.
Не трудно заметить, что для опытов, результаты которых определяются значением отношения заряд/масса тела (а именно в таких опытах проверялась справедливость выводов СТО), утверждения (4) и (6) формально эквивалентны.
То есть такие опыты допускают двойное толкование.
Покажем это на примере движения заряженной частицы в ускорителе.
В рамках (6) напряжённость электрического поля для наблюдателя, который движется в нём со скоростью v, будут описываться так:
Е= E0(1-v2/u2) (7)
где E0 — напряжённость электрического поля в системе отсчёта неподвижного наблюдателя.
Отсюда сила действующая на электрический заряд, движущейся в электрическом поле, с учётом (6) и (7) будет равна:
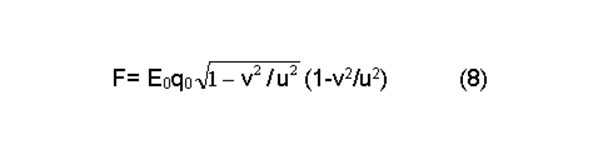
Подставим (8) в правую часть уравнения движения (5). При этом будем считать, что m=m0 , то есть масса ускоряемой частицы является инвариантом. Получим:
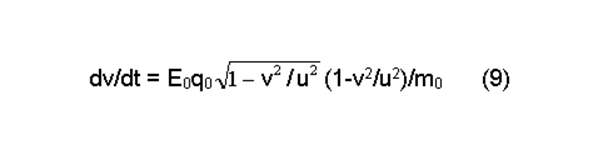
Нетрудно заметить, что для случая u = c уравнения (5) и (9) будут тождественными. Однако смысл их правых частей будет существенно разным.
В соотношении (5) член -
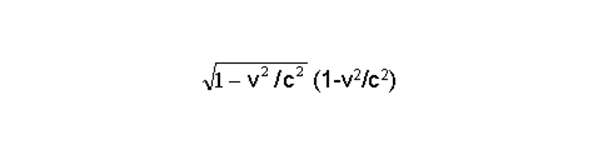
- относится к массе частицы.
Потому при v = c масса частицы становится бесконечно большой, а потому под действием конечной силы ее ускорение будет нулевым.
В соотношении (9) ускорение частицы при v = u также становится нулевым. Но по другой причине. Двигаясь с равными скоростями заряд и ускоряющая его волна перестали взаимодействовать друг с другом.
Формально это выражается в том, что член -
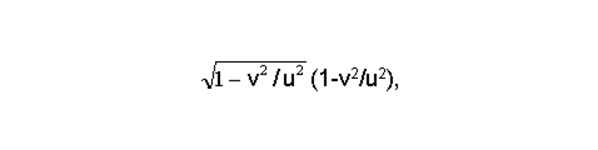
- определяющий заряд частицы и напряженность ускоряющего поля, при v = u обнуляется. То есть ускорение частицы стало нулевым потому, что на нее не действуют никакие силы.
Вернёмся к уравнению (9). Допустим, что частица движется в ускорителе со скоростью v>u. В этом случае член E0(1-v2/u2), то есть напряжённость ускоряющего поля станет отрицательной, а член -
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.