Классификация РПУ по назначению, рабочему диапазону частот, характеру обрабатываемых сигналов и другим признакам, страница 6

Принцип разделимости в селективных каскадах:

Данный пример показывает, что можно рассматривать отдельно частотно-селективные цепи и остальные усилительные элементы (УЭ). Рассчитывать каждую часть по отдельности удобнее, чем все части одновременно (УРЧ).

Частотно-селективные цепи называются фильтрами. Задачи, которые решают фильтры:

1.  Задача частотной селекции сигналов;

2.  Согласование импедансов (комплексных сопротивлений). Межкаскадное согласование.

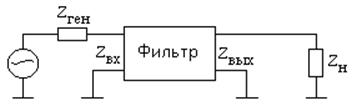
Условия согласования:                1. ;            2. ;                  3. .

Одноконтурный и многоконтурные фильтры в РПУ.

Комплексный коэффициент передачи параллельного колебательного контура:   .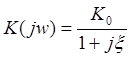

Где 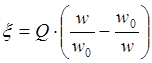 - обобщенная расстройка контура. Ширина спектра определяется добротностью Q.

Добротность Q колебательного контура состоит из собственной добротности Q₀ и эквивалентной добротности Q_Э.

Путем увеличения числа контуров можно улучшить частотную селекцию:

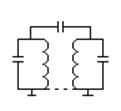
Частотно-селективные свойства зависят от Q_Э.

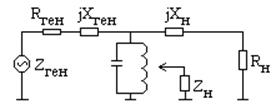
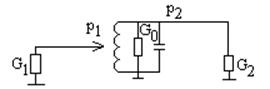
Для решения задач согласования и частотной селекции генератор и нагрузку включают в контур не полностью, чтобы добротность была заданной. Импедансы антенны, усилительных каскадов и других цепей приемника при подключении к ним колебательного контура влияют на настройку и резонансную характеристику этого контура. Если требуется уменьшить это влияние, то применяют неполное включение.

p₁, p₂ – коэффициенты включения, исходя из Q_Э.

Задачи согласования:  Компенсация реактивностей, согласование активных сопротивлений.

Виды связи.

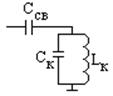
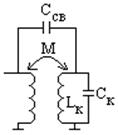
А)   Внешне емкостная связь: (p = 1):

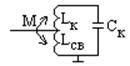
Б)   Трансформаторная связь (индуктивная):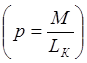  

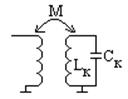
В)   Автотрансформаторная связь: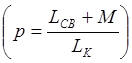  

Г)   Внутри емкостная связь: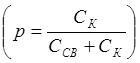  

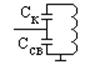
Д)   Комбинированная связь:  

Общие соотношения для одноконтурного фильтра.

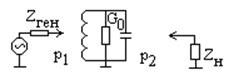
Коэффициент передачи такой цепи: 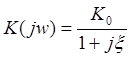  ,   где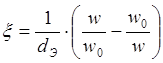  

d_Э – эквивалентное затухание;    Q_Э = 1/d_Э – эквивалентная добротность.

Нашей задачей является найти:   К₀ и d_Э.

Известны:   p₁, p₂, w₀, G₀ – собственная проводимость (определяется потерями).

Пересчитаем генератор и нагрузку в параллельную эквивалентную схему замещения:

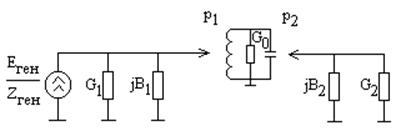
Пересчитаем генератор и нагрузку в контур (частичные включения пересчитываются в контур, как полное включение).

Этот контур должен быть настроен на w₀. Это делается таким образом, что  и  пересчитываются в емкость или индуктивность контура, вследствие чего эти проводимости исключаются.

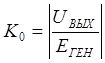  - резонансный коэффициент передачи.     

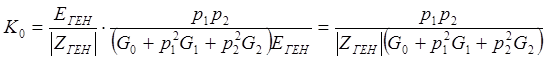
Получим d_Э:

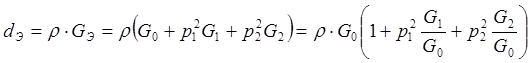 - эквивалентное затухание.

r - характеристическое сопротивление контура.

G_Э – эквивалентная проводимость на резонансной частоте.

rG₀ – собственное затухание в контуре (d₀).

Амплитудно-частотная характеристика:

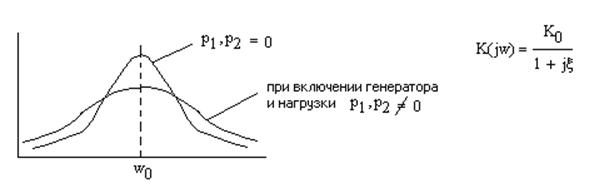
Одноконтурный фильтр в режиме максимального коэффициента передачи.

Требования:

1. Резонансная частота, должна оставаться равной w.
2. Подобрать p₁, p₂ так, чтобы K₀ был максимальным. (- максимум максиморум).
3. Df – не интересует.

Ограничения:   .

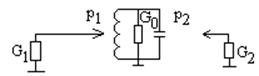
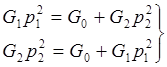 - эти условия совместно не возможны, так как в противном случае должно быть G₀ = 0.

Поэтому, если G₁ > G₂, то с целью увеличения K₀:  p₂ = 1, p₁ – выбираем из условия согласования:

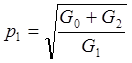               Влияние G₀ ослабляется.

То есть получаем:

1.   Если :           

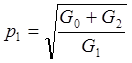
2.   Если :           

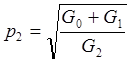
Эти два соотношения определяют условия максимального коэффициента передачи.

Запишем выражения для максимального коэффициента передачи эквивалентного затухания:

;           

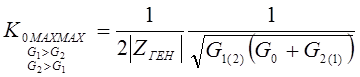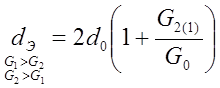
Выводы:

1. Больший коэффициент передачи получить нельзя.
2. Этот режим не всегда реализуем.
3. В данном режиме фильтр обладает очень низкими селективными свойствами.

Использование этого режима:

1. Задача согласования.
2. Задача полной передачи энергии генератора в нагрузку.

Одноконтурный фильтр в режиме максимального коэффициента передачи при заданной полосе пропускания.

Так как фильтр одноконтурный, то его АЧХ определяется добротностью и полосой пропускания контура.

Нашей задачей является спроектировать фильтр, чтобы он обеспечивал заданную полосу пропускания и максимальный коэффициент передачи. В данной задаче являются известными такие параметры, как: