Поисковая оптимизация теплообменного аппарата типа «труба в трубе», страница 3

Основными соотношениями для расчета теплообменников являются: уравнение теплового баланса, Вт

Q = G₁×С_р1×(t₁¢ - t₁¢¢) = G₂×С_р2×( t₂¢¢ - t₂¢),  (2.4)

где G₁, G₂ – расходы, соответственно, теплоотдающего (1) и тепловоспринимающего (2) теплоносителей, кг/с;

С_р1, С_р2 – средние массовые изобарные теплоемкости теплоносителей, Дж/(кг×К);

t₁¢,  t₂¢ – температуры теплоносителей на входе в ТА, °С;

t₁¢¢,  t₂¢¢– температуры теплоносителей на выходе из ТА,  °С;

уравнение теплопередачи, Вт

          Q = k×Dt_ср×F,                                         (2.5)

где k – коэффициент теплопередачи, Вт/(м²×К);

Dt_ср –  среднелогарифмический температурный напор, К;

F – площадь поверхности теплообмена, м²;

уравнение затрат мощности на прокачивание теплоносителей, Вт

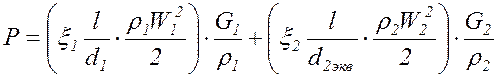,          (2.6)

где  x - коэффициент гидравлического сопротивления;

r₁, r₂ ,   - плотности теплоносителей, кг/м;

W₁, W₂,   - скорости движения теплоносителей, м/с.

l - длина теплообменника, м ;

d₁ - внутренний размер внутренней трубы, м ;

d_2экв - эквивалентный диаметр кольцевого сечения, м.

Значение эквивалентного диаметра определяется по формуле

d_2экв = d_{кольц нар} – d_{кольц.вн}, где d_{кольц нар} – наружный диаметр внутренней трубы, м; d_{кольц.вн} – внутренний, диаметр наружной трубы, м (см. рис. 1);

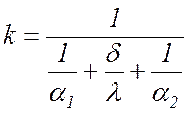,                                       (2.7)

где  a₁, a₂ - коэффициенты теплоотдачи, Вт/(м²×К);

d - толщина стенки воздушной трубы, м;

l - коэффициент теплопроводности материала трубы, Вт/(м×К);

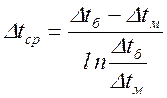,                                       (2.8)

где  Dt_б, Dt_м - наибольшая и наименьшая разницы между температурами теплоносителей, ºС.

Программа предусматривает противоточную схему движения теплоносителей (рис. 4);

F = p×d_расч×l(2.9)

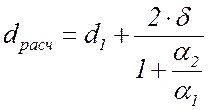.                              (2.10)

Рис. 4.  Схема изменения температур теплоносителей

Здесь использовались приближенные формулы для расчета теплопередачи через тонкостенную цилиндрическую трубу.

Варьируемыми геометрическими характеристиками теплообменника

типа "труба в трубе"  являются  внутренний  диаметр внутренней трубы (d₁) и эквивалентный диаметр кольцевого канала (d_2экв).

Скорости течения теплоносителей определяются из уравнений расхода

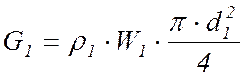                               (2.11)

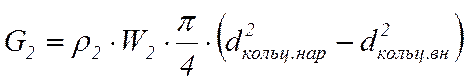         (2.12)

Коэффициенты теплоотдачи и сопротивления трения в трубе и кольцевом канале рассчитываются по следующим формулам:

при  Re³ 10000 (турбулентный режим)

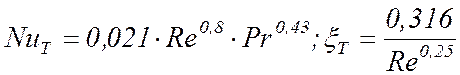;        (2.13)

при    Re£ 2300 (ламинарный режим)

для внутренней трубы

Nu_л = 4; x = 64/Re;                                 (2.14)

для кольцевого канала

Nu_л = 4,34 + 0,78×d_{кольц.нар}/d_{кольц.вн};              (2.15)

при  2300 <Re< 10000 (переходный режим)

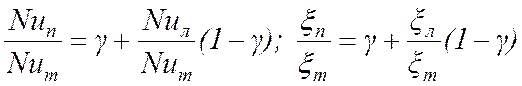,          (2.16)

где   g  - коэффициент перемежаемости.

Коэффициент перемежаемости рассчитывается по формуле:

g  = 1 - ехр(1 - Re/2300),(2.17)

а значения Nu и xпри ламинарном и турбулентном режимахопределяются по приведенным выше формулам.

Каждый этап расчета заканчивается поиском значения целевой функции по (2.3).

Уравнение (2.3) является уравнением поверхности в системе координат d₁, d_2экв, Z.

2.4 Работа с моделью

В рассматриваемой задаче для нахождения оптимального варианта конструкции теплообменника варьируются два параметра  d₁ и d_2экв (в программе соответственно d1 и d2). В связи с этим говорят о двумерной задаче оптимизации. Простейшим методом решения многомерных задач такого типа является метод покоординатного спуска. Его идея заключается в последовательном циклическом применении одномерного поиска для каждого варьируемого параметра. Например, возможна следующая последовательность расчета (см. рис. 5): поиск начинается с базовой точки с координатами  d1 = 0,08м; d2 =0,03м. Сначала осуществляется спуск вдоль 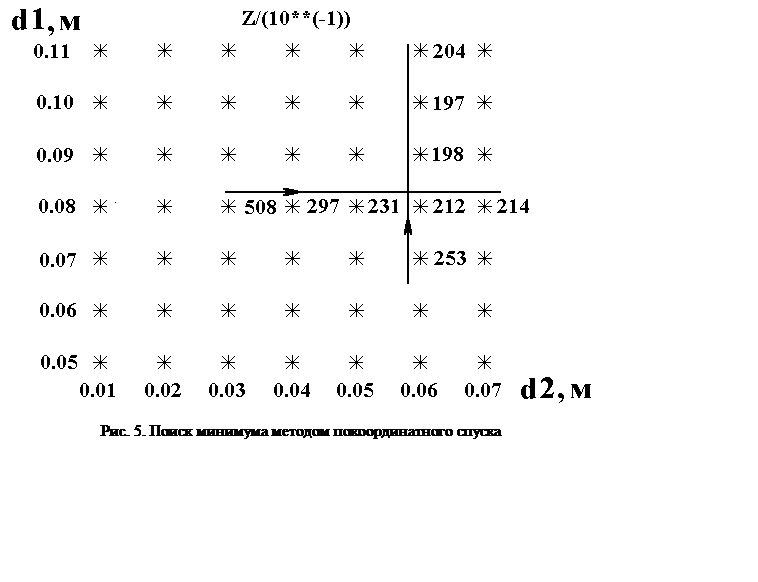 координаты d2при фиксированном значении координаты d1 =  0,08ми в точке d2 =0,06мбыло достигнуто наименьшее значение целевой функции Z = 212. После достижения минимума целевой функции в выбранном направлении производится поиск вдоль оси d1при фиксированном значении d2 = 0,06 м и т.п.

Эти операции повторяются до тех пор, пока любое перемещение из некоторой точки не будет приводить к увеличению целевой функции (возможен только «подъем вверх»). Если необходимо получить более точный результат, эту точку выбирают в качестве базовой и проводят поиск с меньшим шагом.