Спрощене зрівнювання триангуляції. Мета математичної обробки геодезичних мереж, страница 3

На основі геодезичних мереж 1 і 2 класів розвиваються геодезичні мережі 3 і 4 класів. Довжина сторони тріангуляції 3 класи повинна бути не більше 5-8 км, а тріангуляція 4 класи від 2 до 5 км Припустимі нев'язки в сумі кутів трикутників у триангуляції 3 класи не повинні перевищувати 5", а в триангуляції 4 класи 7".

Завершенням робіт зі створення опорної геодезичної мережі — триангуляції, трилатерації, полігонометрії — і нівелюванню всіх класів є складання каталогів, з яких і одержують координати пунктів геодезичної мережі. У каталогах крім назв пунктів, номерів точок, видів і класу геодезичних знаків по їхньому місцезнаходженню вказують для триангуляції: координати X, У и Н кожного пункту мережі із вказівкою системи координат, а також дирекційні кути сторін мережі і їхніх довжин. Для полігонометрії: координати X, У и Н пунктів, дирекційні кути й довжини всіх сторін полігонометрії. Висоти всіх пунктів даються від рівня Кронштадтського футштока.

3. Попереднє обчислення

У відкритій місцевості, для визначення координат розпознаків, користуються методом триангуляції. Він полягає в тому, що на сторонах трикутників державної геодезичної мережі, як на, базисах, будують системи трикутників в яких як правило, міряють всі три кути.

Трикутник

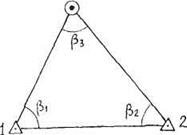
Якщо на місцевості побудувати трикутник, у якого одною вершиною є розпознак "Р" двома другими пунктами триангуляції (полігонометрії) (Рис. 4), і виміряти теодолітом всі кути β₁, β₂, β₃, які повинні бути не менше 30⁰ і не більше 120⁰, то координати розпознака можна обчислити в такій послідовності:

1.  Обчислюють кутову нев'язку в трикутнику (β₁+β₂+β₃) - 180⁰ = f_β, яка не повинна перевищувати ± 1', якщо кути вимірювались оптичним теодолітом  і ±1,5', якщо кути вимірювались 30" теодолітом і виправляють виміряні кути.

2.  За координатами пунктів "1" "2", розв'язуючи обернену геодезичну задачу, визначають дирекційний кут α_1-2 лінії 1-2 і її довжину d_1-2.

3.  За теоремою синусів обчислюють сторони трикутника 1-Р і 2-Р.

4.  Обчислюють дирекційні кути сторін трикутника 1-Р і 2-Р

α_2-Р = α_1-2 - β₁;           α_2-Р = α_1-2 ± 180⁰ + β₂.

5.  По обчислених сторонах і дирекційних кутах сторін трикутника двічі обчислюють координати розпознака.

Рис.4

Геодезичний чотирикутник

Якщо розпізнавальний знак "Р" видно тільки з двох пунктів тріангуляції "1" і "2" (Рис. 5) при цьому, кути на пунктах триангуляції "1" або "2" менші 30°, то користуються допоміжною точкою "С", яку видно із цих пунктів, крім цього з точки "С" повинно бути видно пункти тріангуляції "1" і "2" і розпознак "Р". В такому випадку на всіх точках міряють теодолітом всі кути. Після вимірювання кутів, у кожному трикутнику, обчислюють кутові нев'язки і якщо вони не перевищують допустиму величину виправляють виміряні кути. За координатами вихідних пунктів "1" і 2" і виправлених кутах за формулами Юнга, обчислюють координати допоміжної точки "С", а потім двічі з трикутників 2СР і СІР обчислюють координати розпознака "Р".

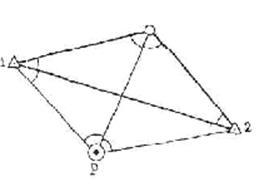Рис. 5

Ланцюг трикутників

В відкритій і напіввідкритій місцевості координати розпознаків можна визначити ланцюгом трикутників.

Для цього необхідно мати на початку ланцюга не менше двох пунктів триангуляції і в кінці ланцюга хоч один, або навпаки (Рис.6). Ланцюгом трикутників можна визначати одночасно координати декількох розпознаків. Так, як між пунктами триангуляції і розпозпаками немає взаємної видимості то зв'язок між ними виконується за допомогою допоміжних точок. На всіх точках ланцюга трикутників теодолітом міряють всі кути і після цього визначають кутові нев'язки в трикутниках. Допустимі кутові нев'язки розподіляють порівну на всі кути трикутника і за формулою Юнга, починаючи від вихідної сторони триангуляції. послідовно від трикутника до трикутника обчислюють координати всіх точок.

Обчисленні координати (окремо абсциси і ординати) виправляють в такий спосіб:

1.  Утворюють різницю "V_n" між двома значеннями координати кінцевого пункту триангуляції обчисленого в даному ланцюгу трикутників, і його значенням взятого з каталога координат пунктів триангуляції.

2.  Змінюють знак одержаної помилки "V_n" па протилежний, ділять її величину на кількість трикутників в ланцюгу "п" і цей результат множать на кількість трикутників "і" між вихідними пунктами триангуляції і розпознаком, положення якого необхідно виправити.

Величина нев'язки в координатах "V_n" кінцевого пункту триангуляції не повинна перевищувати 4 м при зйомці в масштабі 1:10000 і 2 м - при зйомці в масштабі 1:5000.

Рис. 6