На цій схемі в середині кожного полігона, під його номером, заготовляють табличку нев'язок (в міліметрах), а біля кожної ланки - табличку поправок, при цьому по зовнішніх ланках - по одній табличці з зовнішньої сторони, а по внутрішніх ланках - по дві таблички з обох сторін кожної ланки.
Після цього обчислюють з точністю до 0.01 червоні числа для кожної ланки кожного полігона за правилом: червоне число ланки дорівнює числу штативів ланки, поділеному на число штативів всього полігона (або довжині ланки в км поділеному на периметр всього полігона).
Для ланок АВ, ВDі DА першого полігона (Рис.3) відповідно будемо мати такі червоні числа: 0.45, 0.33 і 0.22. Сума червоних чисел в кожному полігоні повинна дорівнювати 1. Червоні числа виписують над відповідними табличками червоним кольором. Безпосередньо на схемі розподіляють нев'язки, починаючи з найбільшої за абсолютною величиною в такій послідовності: множать нев'язку даного полігона послідовно на кожне червоне число його ланки. (В нашому прикладі для III полігона, з якого почали зрівнювання, одержали поправки +25, +8, +14). Одержані добутки записують в зовнішні таблички поправок під відповідними червоними числами з знаком нев'язки і сума всіх добутків повинна дорівнювати величині нев'язки, тобто нев'язці III полігона. На схемі розподілену нев'язку підкреслюють.
|
|
Переходять до сусіднього полігона І. В табличні нев'язок записують під нев'язкою полігона нову, одержану, як алгебраїчну суму нев'язки з поправкою, винесеною за рахунок спільної ланки з сусіднього полігона (+38)+(+8)=(+46). Нову нев'язку множать послідовно на червоні числа кожної ланки даного полігона, і одержані добутки записують в відповідні таблички поправок, контролюючи їх суму, яка повинна дорівнювати величині нев'язки.
Після цього переходять до наступного, II полігона, підраховують його нову нев'язку, в якій враховані внесені за рахунок спільних ланок поправки з сусідніх полігонів (-42)+(+І5)+(+14)=(-13), з цією нев'язкою поступають так само, як описано в попередніх полігонах.
Закінчивши, таким чином, перший круг, переходять знову до початкового полігона. Підраховують його нову нев'язку, яка складається з алгебраїчної суми поправок, внесених з спільних ланок сусідніх полігонів (+10)+(-4)=(+6). Записують її в табличку нев'язок, множать послідовно на червоні числа ланок. Одержані добутки записують в відповідні таблички поправок і контролюють суми добутків. Потім, переходячи послідовно від полігона до полігона, поступають аналогічно до тих пір, поки нев'язки всіх полігонів будуть дорівнювати нулю, тобто будуть винесені за зовнішні межі полігонів.
Після закінчення розподілу нев'язок підраховують алгебраїчну суму поправок в кожній табличці і записують її під подвійною лінією. Обчислюють поправки в сумах перевищень по кожній ланці і записують їх на схемі, в дужках, біля відповідної ланки з внутрішньої сторони полігона.
Поправка в суму перевищень внутрішньої ланки дорівнює алгебраїчній сумі чисел зовнішньої таблички поправок, взятої з протилежним знаком, плюс алгебраїчна сума чисел внутрішньої таблички поправок.
Наприклад, в II полігоні:
для ходу СD поправка буде: -(-4)+(+16)=(+20)
для ходу DВ поправка буде: -(-3)+(+14)=(+17)
для ходу ВС поправка буде: -(-5)+0=(+5)
Обчислені поправки записують в таблицю зрівнювання полігонів, (таблиця 28). Алгебраїчна сума поправок по кожному полігону, повинна дорівнювати величині нев'язки з протилежним знаком.
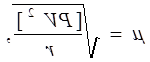 |
де V - поправка в суму перевищень ланки;
Р = 1/n - число, обернене кількості штативів ланки, r - число полігонів.
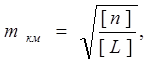 |
|||
|
|
За вихідною відміткою марки А і відповідних сум перевищень з урахуванням поправок обчислюють відмітки вузлових точок В, С, D, контролюючи їх за всіма наявними напрямами
hАВ=+18.583 + (-20)=+18.563 НA =185.215
hBC =-7.711+ (+5) =-7.706 НB =203.778
hCA =-10.829+ (-28) = -10.857 НC =196.072
Σh =0.000 НА =185.215
hBD>= -13.867 + (-17)= -13.884 НD =203.778-13.884 = 189.894
hAD = +4.678 + (-1) = +4.679 НD =185.215 + 4.679 = 189.894
hCD = -6.198 +(-20) =+6.178 НD =196.072-6.178 = 189.894
Обчислення відміток можна виконувати безпосередньо на схемі, або в відомості обчислення відміток.
Способом В.Б.Попова можна зрівнювати також незалежні мережі теодолітних ходів.
Спочатку зрівнюють горизонтальні кути, розподіляючи кутові нев'язки в зімкнутих полігонах пропорціонально червоним числам. Обчислюють зрівняні дирекційні кути і прирости координат. За обчисленими приростами координат підраховують нев'язки в приростах координат в кожному зімкнутому полігоні. Нев'язки в приростах координат розподіляють в зімкнутих полігонах гак, як виконували зрівнювання перевищень в незалежній нівелірній мережі, виконуючи окремо зрівнювання приростів абсцис і приростів ординат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.