Автономні методи визначення азимута. Суть визначення азимута із астрономічних спостережень

Лекція № 24. Автономні методи визначення азимута

       План лекції:

1. Суть визначення азимута із астрономічних спостережень.
2. Небесна сфера і її елементи.

До автономних методів визначення азимута відносяться такі методи, в яких вимірювання на кожному пункті не залежать від результатів вимірювання на інших пунктах.

До автономних методів визначення азимутів відносяться астрономічний та гіроскопічний.

Найбільш точним методом є астрономічний, але його застосування залежить від метеорологічних умов і його неможливо застосувати для орієнтування підземних геодезичних мереж. Найбільш прийнятним і ефективним є гіроскопічний метод. Гіроскопічним методом можна визначати азимут напряму за порівняно короткий час (1-2 години) з точністю 15 "-60". Перевага цього методу полягає в тому, що вимірювання азимута гіроскопічними приладами не залежить від умов погоди, пори року і доби, а також не залежить від густоти геодезичної мережі району робіт.

Визначувані орієнтирні напрями можуть розташовуватися як на поверхні землі, так і в шахтах і інших підземних спорудах.

Спостереження з гіроскопічними приладами порівняно прості і виконуються досить швидко, а процес вимірювання може бути повністю автоматизованим.

Автономні методи визначення азимута застосовують для орієнтування незалежних знімальних мереж, для прив'язки теодолітних і полігонометричних ходів і для підвищення їх точності.

1. Суть визначення азимута із астрономічних спостережень

Азимут " А " напряму ОМ на земний предмет є сума А = а + Qазимута "α" напряму на небесне світило (зірку, Сонце) в певний момент часу "Т" і виміряного в той же час горизонтального кута "Q" між напрямами на світило "δ" і земний предмет "М". (Рис. 1).

Рис. 1

Азимут світила не може бути виміряний безпосередньо, тому що напрям астрономічного меридіану ОN не відмічений на місцевості. Азимут "α" можна обчислити, попередньо вимірявши висоту світила над горизонтом або середній момент часу вимірювання горизонтального кута "Q". Дійсно, спостерігаючи небесні світила з даної точки, можна помітити, що положення їх на небесній сфері з плином часу постійно змінюється за висотою і за азимутом. Очевидно, існує залежність, яка дозволяє визначати азимут "α", який відповідає, часу вимірювання горизонтального кута "Q".

Таким чином, суть визначення астрономічного азимута напряму на земний предмет полягає в обчислені астрономічного азимута "α" на момент часу, коли вимірювався горизонтальний кут між напрямами на світило і місцевий предмет.

Для визначення азимута напряму з астрономічних спостережень необхідно розглядати кути і трикутники, які розташовані на сферичній поверхні, тому розглянемо попередньо необхідні формули для розв'язання сферичних трикутників. Якщо на кулі (Рис.2) АВА₁В₁з центром в точці О взяти три точки А, В, і С і провести через кожні дві із них дуги великих кругів АСА₁С₁ ВСВ₁С₁ і АВА₁В₁, то утворений такими дугами великих кругів трикутник АВС називається сферичним трикутником. Сферичним кутом називається кут, утворений на сфері перетином двох дуг великих кругів. Наприклад, сферичний кут САВ утворений перетином дуг великих кругів АВА₁В₁ і АСА₁С₁. Точки А, В і С, перетин дуг великих кругів на сфері, називаються вершинами сферичних кутів, а дуги АВ, ВС і АС великих кругів, які знаходяться між вершинами кутів називаються сторонами трикутника. Кути сферичного трикутника позначаються, аналогічно плоскій тригонометрії, великими літерами, якими позначено вершини трикутника, а сторони – малими літерами, відповідно протилежним кутам (див. Рис. 2).

Рис. 2

Сторони сферичного трикутника є дугами так само, як і кути будуть виражатися в градусах, мінутах і секундах. Сторони сферичного трикутника можна виразити лінійною мірою, якщо відомий радіус сфери. В сферичному трикутнику сума кутів завжди більша 180⁰ і менша 540⁰. Якщо в сферичному трикутнику один кут дорівнює 90⁰, то такий трикутник називається прямокутним. Сферичний трикутник має шість елементів – три кути і три сторони. Трикутник можна розв'язати, якщо відомі три будь-які елементи трикутника.

Сферичний трикутник АВС (Рис. 2) можна розв'язати за одною із формул сферичної тригонометрії.

Теорема синусів для сферичного трикутника

Синуси сторін трикутника пропорціональні синусам протилежних кутів.

Формула косинуса сторін сферичного трикутника

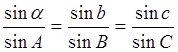Косинус сторони сферичного трикутника дорівнює добутку косинусів двох інших його сторін доданого до добутку синусів тих же сторін на косинус кута між ними.

cos α =cos c cos b +sin c sin b cos A,

cos b=cos c cos α +sin c sin α cos B,

cos c=cos α cos b + sin α sin b cos C.

Формула косинуса кута сферичного трикутника

Косинус кута сферичного трикутника дорівнює добутку косинусів двох інших кутів, взятого з протилежним знаком, доданого до добутку синусів тих же кутів на косинус сторони між ними.

cos A = -cos C cos B + SinCsin B cos α,

cos B = -cos A cos C + SinAsin C cos b,

cos C = -cos A cos B + SinAsin B cos c.

Для визначення астрономічних широт, довгот і азимутів астрономічними методами спостерігають Сонце або зорі. Величини зірок домовились характеризувати числами, при цьому найслабші, які видно неозброєним оком, це зорі шостої величини.

Всі зорі, різні за величиною на небесній сфері об'єднані в сузір'я, назви яких нагадують персонажі або події античної міфології.

Окремі зорі сузір'я позначають буквами грецької азбуки або просто номерами.