Основные методики анализа финансовых результатов предприятия

явления и формулируемые на естественном языке (вербальное описание) в терминах «много больше», «много меньше», «приблизительно равно» и т. д. Формализация качественной информации может выполняться на базе двухзначной или нечеткой логики. При использовании двухзначной логики возможны всего два варианта: «О» - вне множества: «1» - на множестве. Применение аппарата теории нечетких множеств в большей степени соответствует процессу прогнозирования различных явлений и описанию их на естественном языке.

Пусть имеются последние данные об основных источниках получения прибыли предприятием, X: X₁ - финансовый результат от реализации товаров; X₂ - финансовый результат от прочей реализации; X₃ - финансовый результат от внереализационных операций. Предполагается, что предприятие не получает убытков.

Общая прибыль определяется в этом случае следующим образом:

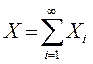                                              .                                                     (3.25)

Прогнозное значение общей прибыли предприятия (X*) определяется на основании прогнозирования темпов изменения (прироста или снижения) каждого источника получения прибыли ():

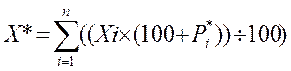                                     .                             (3.26)

Введем лингвистическую переменную I- = «темп изменения прибыли» с базовыми значениями Т ={T_i}  = {большое снижение; среднее снижение; малое снижение; малый прирост; средний прирост; большой прирост} и числовой областью определения U = [-100; 300]%. Связь лингвистического описания с его количественным значением задается функцией принадлежности фактора нечеткому множеству. Таким образом, терм-множество лингвистической переменной «темп изменения прибыли» состоит из шести нечетких подмножеств (компонентов) и каждому из них соответствует своя функция принадлежности μ_Ti(u). Интерпретацией степени принадлежности является субъективная мера того, насколько элемент u  соот­ветствует понятию, смысл которого формализуется нечетким множеством Т_i .

Методам и процедурам построения функции принадлежности посвящены труды ряда ученых и к каждому из методов формулируются свои требования и обоснования по их конкретному выбору /10, 11/. Как отмечает Дюбуа Д. и Прад А., Заде Л. А. /12/ на практике можно задать приближенное представление функции принадлежности, которое достаточно для реальных приложений, так как большая точность здесь не требуется. Для целей прогнозирования суммы ожидаемой прибыли применим прямой метод, заключающиеся в том, что эксперт непосредственно задает правила определения значений функции принадлежности, характеризующей темп изменения прибыли.

Построение функций принадлежности каждого элемента терм-множества «темп изменения прибыли» производится на основании обработки оценок группы экспертов, каждый из которых задает функцию принад­лежности как совокупность пар

                                     T={ μ_T(u)/(u)},                                                       (3.27)

указывая наиболее приемлемые по его мнению значения u (μ_T(u)=1) и значения u ниже и выше которых величина не может изменяться (μ_T(u)=0).

Для получения обобщенного (комплексного) мнения экспертов могут