Интерполяция промежуточных точек прямой

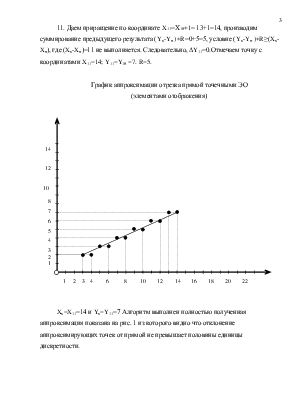
Задание.

Произвести интерполяцию промежуточных точек прямой, заданной координатами (X_н=3, Y_н=2, X_к=14, Y_к=7).

Решение:

         1. В соответствии с алгоритмом отмечаем начальную точку с координатами X_н; Y_н (рис. 1).

Определяем (X_к-X_н)=14 – 3=11 и (Y_к-Y_н)=7 – 2=5

Даем единичное приращение по координате X₁=Х_н+1=3+1=4 и производим суммирование значения (X_к-X_н)/2+(Y_к-Y_н)=11/2+5=10,5, учитывая что формула Y_i=Y_н+INT(1/2+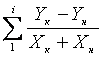), где INT означает, что берется целая часть результата, полученная в круглых скобках. Получаем R=10 сравнивая полученные значения c (X_к-X_н)=11. Так как (X_к-X_н)/2+(Y_к-Y_н)=11/2+5=10,5=10<(X_к-X_н)=11, то ∆Y₁=0. Отмечаем точку с координатами X₁=4; Y₁= Y_н =2 (R=10).

         2. Даем приращение по координате X₂= X₁+1= 4+1=5, производим

суммирование предыдущего результата (Y_к-Y_н )+R=5+10=15, условие 

(Y_к-Y_н )+R≥(X_к-X_н), где (X_к-X_н)=11 выполняется. Следовательно, ∆Y₂=1. Отмечаем точку с координатами X₂=5; Y₂= Y₁+1=2+1=3. Вычитаем из (Y_к-Y_н )+R – (X_к-X_н)

15 – 11=4,  получаем остаток R=4.

         3. Даем приращение по координате X₃= X₂+1= 5+1=6, производим

суммирование предыдущего результата (Y_к-Y_н )+R=4+5=9, условие 

(Y_к-Y_н )+R≥(X_к-X_н), где (X_к-X_н)=11 не выполняется. Следовательно, ∆Y₃=0. Отмечаем точку с координатами X₃=6; Y₃= Y₂=3.R=9.

         4. Даем приращение по координате X₄= X₃+1=6+1=7, производим

суммирование предыдущего результата (Y_к-Y_н )+R=9+5=14, условие 

(Y_к-Y_н )+R≥(X_к-X_н), где (X_к-X_н)=11 выполняется. Следовательно, ∆Y₃=1. Отмечаем точку с координатами X₄=7; Y₄= Y₃+1=3+1=4. Вычитаем из (Y_к-Y_н )+R – (X_к-X_н)

14 – 11=3,  получаем остаток R=3.

         5. Даем приращение по координате X₅= X₄+1=7+1=8, производим

суммирование предыдущего результата (Y_к-Y_н )+R=3+5=8, условие 

(Y_к-Y_н )+R≥(X_к-X_н), где (X_к-X_н)=11не выполняется. Следовательно, ∆Y₃=0. Отмечаем точку с координатами X₅=8; Y₅= Y₄=4. R=8.

         6. Даем приращение по координате X₆=Х₅+1= 8+1=9, производим суммирование предыдущего результата (Y_к-Y_н )+R=8+5=13, условие (Y_к-Y_н )+R≥(X_к-X_н), где (X_к-X_н)=11 выполняется. Следовательно, ∆Y₆=1. Отмечаем точку с координатами X₆=9; Y₆=Y₅+1=4+1= 5. Вычитаем из (Y_к-Y_н )+R – (X_к-X_н)

13 – 11=2,  получаем остаток R=2.

         7. Даем приращение по координате X₇=Х₆+1= 9+1=10, производим суммирование предыдущего результата (Y_к-Y_н )+R=2+5=7, условие (Y_к-Y_н )+R≥(X_к-X_н), где (X_к-X_н)=11 не выполняется. Следовательно, ∆Y₇=0. Отмечаем точку с координатами X₇=10; Y₇=Y₆=5. R=7.