угловая скорость звена направлена по ходу часовой стрелки, векторы L1 и L0 не зависят от обобщенной координаты, в итоге получаем:
Вычтем из каждого угла j3 и получим:
L1sin(j1-j3)- L’3=0
-L1cos(j1-j3)-L3j’3=0
L’3=L1sin(j1-j3)
j’3=-L1cos(j1-j3)/L3
L’3=0,16×sin(115,62-97,57)= 0,0496 м/с.
j’3=-0,16×cos(115,62-97,57)/0,5251=-0,2897
Для нахождения аналогов скоростей звеньев второго контура надо продифференцировать по обобщенной координате систему уравнений 2.2, так как j6 =90, то cos(j6)=0, векторы L6, L3 не зависят от обобщенной координаты, система уравнений имеет вид:
L’7sin(j7)+ L’7j’7cos(j7)-L3 cos(j3)j’3 =0
L’7cos(j7)-L’7 j’7sin(j7)+ L3 j’3sin(j3)=0 (2.7)
Вычтем из каждого угла угол j7 и получим:
L7j’7 -L3
cos(j3-j7)j’3
=0
L’7+L3sin(j3-j7)j’3=0
L’7=-L3 sin(j3-j7)j’3
j’7= (L3cos(j3-j7)j’3)/ L’7
L’7=-0,68×
sin(97,57-164,96) ×(-0,2897)=-0,182 м/с
j’7= (0,68×cos(97,57-194,96) ×(-0,2897))/(-0,182)=-0,816
Для нахождения аналогов скоростей звеньев третьего контура надо продифференцировать по обобщенной координате систему уравнений 2.3, так как j5=180, следовательно, sin(j5)=0, cos(j5)=-1, вектор L4 не зависит от обобщенной координаты, тогда система уравнений примет следующий вид:
L4j’4cos(j4)-
L’7sin(j7)-L7 cos(j7)j’7
=0
-L4j’4sin(j4)+L’5 –L’7 cos(j7)+ L7 j’7sin(j7)=0 (2.8)
j’4=(L’7sin(j7)+L7 cos(j7)j’7)/
(L4cos(j4))
L’5=L4j’4sin(j4)+L’7 cos(j7)- L7 j’7sin(j7)
j’4=(0,816×sin(164,96)+,093×cos(164,96) ×(-0,816))/(0,24×cos(5,76))=0,108
L’5=0,24×0,108×sin(5,76)+(-0,182)×cos(164,96)- 0,093×(-0,816) ×sin(164,96) = =0,183м/с
Аналоги скоростей
центров масс звеньев 3 и 4 получаем в проекциях на оси координат, дифференцируя
по обобщенной координате уравнения 2.4 и 2.5:
S’3X =LO2S3j’3 sin(j3)
S’3Y =-LO2S3 j’3cos(j3) (2.9)
S’3X =0.34×(-0,2897) ×sin(97,57)=-0,097
S’3Y =-0,34 ×(-0,2897) ×cos(97,57) =-0,013
S’4X= -LCS4j’4 sin(j4)- L’5 cos(j5)
S’4Y= LCS4 j’4 cos(j4)- L’5 sin(j5) (2.10)
S’4X= -0,12×0,108×sin(5,76) – 0,183×cos(180) = 0,181
S’4Y= 0,12× 0,108×cos(5,76) – 0,183×sin(180) =0,013
Аналог скорости центра масс звена 5 (S’5X ) равен аналогу скорости звена 5 (L’5): S’5X=0,183
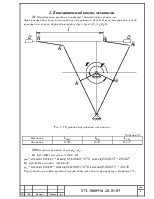
2.7 Находим ускорения звеньев.
Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (2.6), (2.7) и (2.8):
L1j’1cos(j1)-L’’3cos(j3)+L’3sin(j3)j’3+L’3sin(j3)j’3+L3cos(j3)(j’3)2+ L3sin(j3)
j’’3=0
-L1j’1sin(j1)-L’’3sin(j3)-L’3cos(j3)j’3 -L’3cos(j3)j’3+L3sin(j3)(j’3)2-L3cos(j3)j’’3=0
Если мы из каждого угла вычтем угол j3 ,то получим:
-L1cos(j1-j3)-L’’3 +L3 (j’3)2=0
L1sin(j1-j3)-2L’3 j’3 -L3 j’’3=0
L’’3= -L1cos(j1-j3)+
L3 (j’3)2
j’’3=(L1sin(j1-j3)-2L’3 j’3)/L3
L’’3= -0,16×cos(115,62-97,57)+ 0,5251× (-0,2897)2= - 0,108 м/с2
j’’3=(0,16×sin(115,62-97,57)-2×0,0496× (-0,2897))/0,5251=0,397
L”7sin(j7)+L’7 j’7cos(j7)+ L7 j”7cos(j7) + L’7 j’7cos(j7) - L7 (j’7 )2sin(j7)-
L3j”3
cos(j3) + L3 (j’3)2sin(j3)=0
L”7cos(j7)- L’7j’7sin(j7)- L7j”7sin(j7)- L’7j’7sin(j7)- L7(j’7 )2cos(j7)+L3 sin(j3)j”3 - - L3(j’3)2cos(j3)=0
Если мы из каждого угла вычтем угол j7 , то получим:
L’7 j’7
+ L7 j”7 + L’7 j’7 - L3j”3cos(j3-j7) + L3 (j’3)2sin(j3-j7)=0
L”7 - L7(j’7 )2+L3 sin(j3-j7)j”3 - L3(j’3)2cos(j3-j7)=0
L”7= L7(j’7 )2-L3 sin(j3-j7)j”3 - L3(j’3)2cos(j3-j7)
j”7=( L3j”3cos(j3-j7) - L3 (j’3)2sin(j3-j7)-2L’7 j’7 )/L7
L”7= 0, 093×(-0,816 )2-0,68×sin(97,57-164,96) ×0,0397 – 0,68× (-0,2897) ×cos(97,57-
-164,96)=0,065 м/с2
j”7=(0,68×0,0397×cos(97,57-164,96) – 0,68× (-0,2897)2×sin(97,57-164,96)-2×(0,182)
×(-0,816))/0,093= -2,52
L4j’4cos(j4)-
L’7sin(j7)-L7 cos(j7)j’7
=0
-L4j’4sin(j4)+L’5 –L’7 cos(j7)+ L7 j’7sin(j7)=0
L4j”4cos(j4)-
L4(j’4)2 sin(j4)
– L”7sin(j7)-L’7 cos(j7)j’7 -
L7 cos(j7)j”7 – L’7
cos(j7)
j’7 - L7 sin(j7)(j’7 )2=0
-L4j”4sin(j4) -L4 (j’4 )2cos(j4)+L”5 –L”7 cos(j7)+ L7 j’7sin(j7)+ L’7 j’7sin(j7)+ L7 j”7sin(j7)+ L7 (j’7 )2cos(j7)=0
Если мы из каждого угла вычтем угол j4 , то получим:
L4j”4 –
L”7sin(j7 -j4)-L’7 cos(j7 -j4)j’7 - L7 cos(j7 -j4)j”7 – L’7 cos(j7 -j4)j’7 - L7 sin(j7 -j4)(j’7 )2=0
-L4 (j’4 )2+L”5 –L”7 cos(j7 -j4)+ L7 j’7sin(j7 -j4)+ L’7 j’7sin(j7 -j4)+ L7 j”7sin(j7-j4)+ L7 (j’7 )2cos(j7 -j4)=0
j”4=(L”7sin(j7 -j4)+2L’7
cos(j7 -j4)j’7
+ L7 sin(j7 -j4)(j’7
)2)/ L4
L”5=L4(j’4 )2+L”7 cos(j7 -j4)-2L’7 j’7sin(j7 -j4)-L7 j”7sin(j7-j4)-L7 (j’7 )2cos(j7 -j4)
j”4=((-2,52)×sin(164,96 -5,76)+2×(-0,182) × cos(164,96
-5,76)
×(-0,816)+ 0,093× sin(164,96 -5,76) ×(-0.816)2 )/ 0,24= -0.969
L”5=0,24× (0,108 )2+0,065× cos(164,96 -5,76)- 2×0,093×(-0,816) ×sin(164,96 -5,76)- - 0,093×(-2,52) ×sin(164,96-5,76)-0,093× (-0,816 )2×cos(164,96-5,76)= -0,077м/с2
Дифференцируя по обобщенной координате уравнения (2.9) и (2.10), устанавливаем аналоги ускорений центров масс звеньев 3 и 4 в проекциях на оси координат:
S”3X =LO2S3j”3 sin(j3)+ LO2S3(j’3)2 cos(j3)
S”3Y = -LO2S3 j”3cos(j3)+ LO2S3(j’3)2 sin(j3)
S”3X =0,34×0,039× sin(97,57)+ 0,34× (-0,2897)2 cos(97,57)=0,0096
S”3Y = -0,34×0,039×cos(97,57)+ 0,34× (-0,2897)2 sin(97,57)=0,03
S”4X= -LCS4j”4 sin(j4) -LCS4(j’4)2 cos(j4)-
L”5 cos(j5)
S”4Y= LCS4 j”’4 cos(j4) -LCS4(j’4)2 sin(j4)- L”5 sin(j5)
S”4X= -0,12×(-0,969)×sin(5,76)-0,12×(0,108)2×cos(5,76)-(-0,077)×cos(180)= -0,067
S”4Y= 0,12× (-0,969) × cos(5,76) -0,12× (0,108)2× sin(5,76)- (-0,077) × sin(180)=-0,116
2.4 Графическое определение положений, скоростей,
ускорений звеньев механизма.
2.4.1 Алгоритм графического построения планов положений.
Построение планов положениё производим следующим образом.
1. Выбираем масштабный коэффициент длин m= 0.001 м/мм и рассчитываем
чертёжные размеры звеньев табл.2.1
Таблица 2.1
|
О1А, мм |
О2В, мм |
ВС, мм |
У, мм |
|
100 |
1270 |
440 |
550 |
2. Отмечаем на чертеже неподвижные точки О1, О2 , рисуем в них вращательные
кинематические пары;
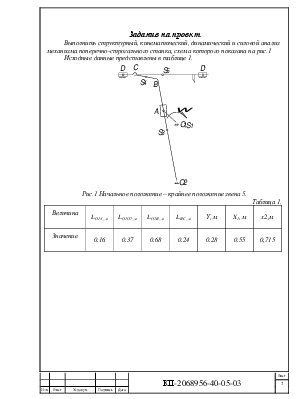
3. На расстоянии У от точки О1 проводим траекторию движения ползуна 5;
4. Проводи окружность О1А, которая является траекторией движения точки А;
5. На траектории движения точки А отмечаем крайние положения кулисы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.